Regresi softmax

Diperbarui 2020-02-12 Baca 3 menit

Ringkasan

Regresi softmax menggeneralisasi regresi logistik ke kasus multikelas dengan menghasilkan probabilitas untuk semua kelas secara bersamaan.
Keluaran berada di rentang $[0, 1]$ dan jumlahnya 1, sehingga mudah dipakai dalam penentuan ambang, aturan berbasis biaya, maupun pipeline lanjutan.
Pelatihan meminimalkan loss entropi silang, langsung mengoreksi perbedaan antara distribusi yang diprediksi dan distribusi sebenarnya.
Di scikit-learn, LogisticRegression(multi_class="multinomial") menyediakan implementasi regresi softmax dan mendukung regularisasi L1/L2.

Intuisi #

Metode ini dipahami lewat asumsi dasarnya, karakteristik data, dan dampak pengaturan parameter terhadap generalisasi.

Penjelasan Rinci #

Formulasi matematis #

Misalkan terdapat $K$ kelas, dengan parameter $\mathbf{w}_k$ dan $b_k$ untuk kelas $k$. Maka

$$ P(y = k \mid \mathbf{x}) = \frac{\exp\left(\mathbf{w}_k^\top \mathbf{x} + b_k\right)} {\sum_{j=1}^{K} \exp\left(\mathbf{w}_j^\top \mathbf{x} + b_j\right)}. $$

Fungsi objektifnya adalah loss entropi silang

$$ L = - \sum_{i=1}^{n} \sum_{k=1}^{K} \mathbb{1}(y_i = k) \log P(y = k \mid \mathbf{x}_i), $$

dengan opsi menambahkan regularisasi untuk menekan overfitting.

Eksperimen dengan Python #

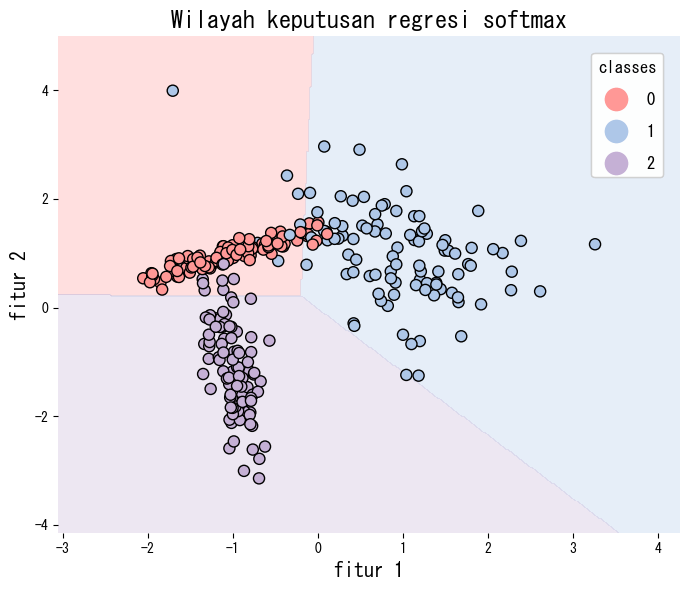
Cuplikan berikut melatih regresi softmax pada data sintetis tiga kelas dan memvisualisasikan wilayah keputusannya. Mengaktifkan parameter multi_class="multinomial" sudah cukup untuk memakai formulasi softmax.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

def run_softmax_regression_demo(
    n_samples: int = 300,
    n_classes: int = 3,
    random_state: int = 42,
    label_title: str = "Wilayah keputusan regresi softmax",
    xlabel: str = "fitur 1",
    ylabel: str = "fitur 2",
) -> dict[str, float]:
    """Train a softmax regression model and visualise decision regions."""
    japanize_matplotlib.japanize()
    X, y = make_classification(
        n_samples=n_samples,
        n_features=2,
        n_informative=2,
        n_redundant=0,
        n_clusters_per_class=1,
        n_classes=n_classes,
        random_state=random_state,
    )

    clf = LogisticRegression(multi_class="multinomial", solver="lbfgs")
    clf.fit(X, y)

    accuracy = float(accuracy_score(y, clf.predict(X)))

    x1_min, x1_max = X[:, 0].min() - 1.0, X[:, 0].max() + 1.0
    x2_min, x2_max = X[:, 1].min() - 1.0, X[:, 1].max() + 1.0
    grid_x1, grid_x2 = np.meshgrid(
        np.linspace(x1_min, x1_max, 400),
        np.linspace(x2_min, x2_max, 400),
    )
    grid_points = np.c_[grid_x1.ravel(), grid_x2.ravel()]
    preds = clf.predict(grid_points).reshape(grid_x1.shape)

    cmap = ListedColormap(["#ff9896", "#98df8a", "#aec7e8", "#f7b6d2", "#c5b0d5"])
    fig, ax = plt.subplots(figsize=(7, 6))
    ax.contourf(grid_x1, grid_x2, preds, alpha=0.3, cmap=cmap, levels=np.arange(-0.5, n_classes + 0.5, 1))
    scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolor="k", cmap=cmap)
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    ax.set_title(label_title)
    legend = ax.legend(*scatter.legend_elements(), title="classes", loc="best")
    ax.add_artist(legend)
    fig.tight_layout()
    plt.show()

    return {"accuracy": accuracy}

metrics = run_softmax_regression_demo(
    label_title="Wilayah keputusan regresi softmax",
    xlabel="fitur 1",
    ylabel="fitur 2",
)
print(f"Akurasi pelatihan: {metrics['accuracy']:.3f}")

Mengaktifkan parameter multi_class=“multinomial” sudah cukup… (diagram)

Referensi #

Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.
Murphy, K. P. (2012). Machine Learning: A Probabilistic Perspective. MIT Press.