Gaussian Mixture Model (GMM)

Diperbarui 2020-03-25 Baca 3 menit

Ringkasan

GMM memodelkan data sebagai gabungan berbobot dari distribusi normal multivariat.
Matriks tanggung jawab (responsibility) menunjukkan seberapa kuat setiap komponen menjelaskan tiap sampel.
Parameter diperkirakan menggunakan algoritma EM; bentuk kovarians dapat dipilih dari full, tied, diag, atau spherical.
Pemilihan model biasanya menggabungkan BIC/AIC dengan beberapa inisialisasi acak agar hasil stabil.

Intuisi #

Metode ini dipahami lewat asumsi dasarnya, karakteristik data, dan dampak pengaturan parameter terhadap generalisasi.

Penjelasan Rinci #

Rumusan #

Kerapatan $\mathbf{x}$ dinyatakan sebagai

$$ p(\mathbf{x}) = \sum_{k=1}^{K} \pi_k \, \mathcal{N}(\mathbf{x} \mid \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k), $$

dengan bobot campuran $\pi_k$ (tidak negatif dan berjumlah 1). Algoritma EM melakukan:

E-step: menghitung tanggung jawab $\gamma_{ik}$. $$ \gamma_{ik} = \frac{\pi_k \, \mathcal{N}(\mathbf{x}_i \mid \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)} {\sum_{j=1}^K \pi_j \, \mathcal{N}(\mathbf{x}_i \mid \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)}. $$
M-step: memperbarui $\pi_k, \boldsymbol{\mu}_k, \boldsymbol{\Sigma}k$ menggunakan $\gamma{ik}$ sebagai bobot.

Log-likelihood meningkat monoton hingga mencapai optimum lokal.

Contoh Python #

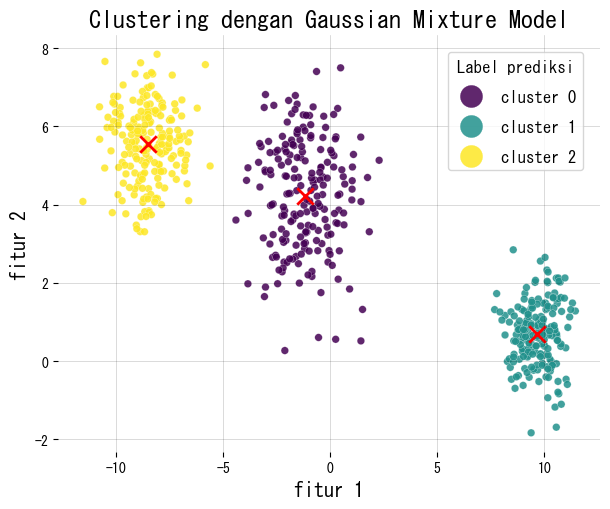
Kita akan menyesuaikan GMM pada data sintetis 2D, menggambar penugasan keras, serta melaporkan bobot campuran dan ukuran matriks tanggung jawab.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
from __future__ import annotations

import matplotlib.pyplot as plt
import numpy as np
from numpy.typing import NDArray
from sklearn.datasets import make_blobs
from sklearn.mixture import GaussianMixture

def jalankan_demo_gmm(
    n_samples: int = 600,
    n_komponen: int = 3,
    cluster_std: list[float] | tuple[float, ...] = (1.0, 1.4, 0.8),
    covariance_type: str = "full",
    random_state: int = 7,
    n_init: int = 8,
) -> dict[str, object]:
    """Melatih GMM dan memvisualisasikan pusat komponen serta label prediksi."""
    fitur, _ = make_blobs(
        n_samples=n_samples,
        centers=n_komponen,
        cluster_std=cluster_std,
        random_state=random_state,
    )

    gmm = GaussianMixture(
        n_components=n_komponen,
        covariance_type=covariance_type,
        random_state=random_state,
        n_init=n_init,
    )
    gmm.fit(fitur)

    label_keras = gmm.predict(fitur)
    tanggung_jawab = gmm.predict_proba(fitur)
    log_likelihood = float(gmm.score(fitur))
    bobot = gmm.weights_

    fig, ax = plt.subplots(figsize=(6.2, 5.2))
    sebar = ax.scatter(
        fitur[:, 0],
        fitur[:, 1],
        c=label_keras,
        cmap="viridis",
        s=30,
        edgecolor="white",
        linewidth=0.2,
        alpha=0.85,
    )
    ax.scatter(
        gmm.means_[:, 0],
        gmm.means_[:, 1],
        marker="x",
        c="red",
        s=140,
        linewidth=2.0,
        label="Pusat komponen",
    )
    ax.set_title("Clustering dengan Gaussian Mixture Model")
    ax.set_xlabel("fitur 1")
    ax.set_ylabel("fitur 2")
    ax.grid(alpha=0.2)
    handles, _ = sebar.legend_elements()
    label_legenda = [f"cluster {idx}" for idx in range(n_komponen)]
    ax.legend(handles, label_legenda, title="Label prediksi", loc="upper right")
    fig.tight_layout()
    plt.show()

    return {
        "log_likelihood": log_likelihood,
        "weights": bobot.tolist(),
        "responsibilities_shape": tanggung_jawab.shape,
    }

hasil = jalankan_demo_gmm()
print(f"log-likelihood: {hasil['log_likelihood']:.3f}")
print("bobot campuran:", hasil["weights"])
print("ukuran matriks tanggung jawab:", hasil["responsibilities_shape"])

Kita akan menyesuaikan GMM pada data sintetis 2D, menggambar… (diagram)

Referensi #

Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.
Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of the Royal Statistical Society, Series B.
scikit-learn developers. (2024). Gaussian Mixture Models. https://scikit-learn.org/stable/modules/mixture.html