Regresi Linear Bayesian

Diperbarui 2020-04-08 Baca 4 menit

Ringkasan

Regresi linear Bayesian memperlakukan koefisien sebagai variabel acak sehingga dapat memperkirakan prediksi beserta ketidakpastiannya.
Distribusi posterior diperoleh secara analitik dari prior dan likelihood sehingga tetap andal pada data yang sedikit atau bising.
Distribusi prediktif berbentuk Gaussian, sehingga mean dan variansinya mudah divisualisasikan untuk mendukung pengambilan keputusan.
BayesianRidge di scikit-learn menyesuaikan varians noise secara otomatis sehingga implementasi praktis menjadi sederhana.

Intuisi #

Metode ini dipahami lewat asumsi dasarnya, karakteristik data, dan dampak pengaturan parameter terhadap generalisasi.

Penjelasan Rinci #

Formulasi matematis #

Misalkan vektor koefisien $\boldsymbol\beta$ memiliki prior Gaussian multivariat dengan mean 0 dan varians $\tau^{-1}$, serta noise observasi $\epsilon_i \sim \mathcal{N}(0, \alpha^{-1})$. Distribusi posteriornya adalah

$$ p(\boldsymbol\beta \mid \mathbf{X}, \mathbf{y}) = \mathcal{N}(\boldsymbol\beta \mid \boldsymbol\mu, \mathbf{\Sigma}) $$

dengan

$$ \mathbf{\Sigma} = (\alpha \mathbf{X}^\top \mathbf{X} + \tau \mathbf{I})^{-1}, \qquad \boldsymbol\mu = \alpha \mathbf{\Sigma} \mathbf{X}^\top \mathbf{y}. $$

Distribusi prediktif untuk masukan baru $\mathbf{x}*$ juga Gaussian, $\mathcal{N}(\hat{y}, \sigma_^2)$. BayesianRidge mengestimasi $\alpha$ dan $\tau$ langsung dari data sehingga tidak perlu disetel manual.

Eksperimen dengan Python #

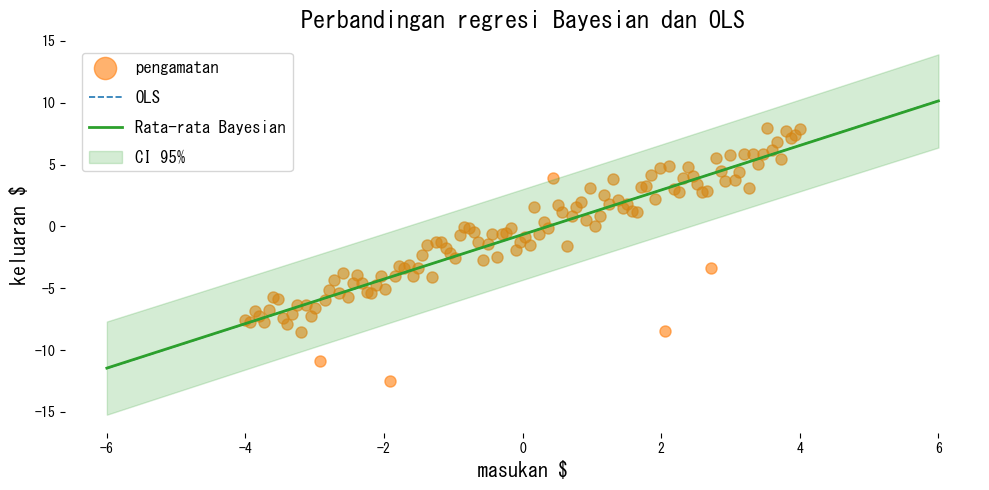
Contoh berikut membandingkan mínimos kuadrat biasa dan regresi linear Bayesian pada data yang mengandung outlier.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import BayesianRidge, LinearRegression
from sklearn.metrics import mean_squared_error

def run_bayesian_linear_demo(
    n_samples: int = 120,
    noise_scale: float = 1.0,
    outlier_count: int = 6,
    outlier_scale: float = 8.0,
    label_observations: str = "observations",
    label_ols: str = "OLS",
    label_bayes: str = "Bayesian mean",
    label_interval: str = "95% CI",
    xlabel: str = "input $",
    ylabel: str = "output $",
    title: str | None = None,
) -> dict[str, float]:
    """Fit OLS and Bayesian ridge to noisy data with outliers, plotting results.

    Args:
        n_samples: Number of evenly spaced sample points.
        noise_scale: Standard deviation of Gaussian noise added to the base line.
        outlier_count: Number of indices to perturb strongly.
        outlier_scale: Standard deviation for the outlier noise.
        label_observations: Legend label for observations.
        label_ols: Label for the ordinary least squares line.
        label_bayes: Label for the Bayesian posterior mean line.
        label_interval: Label for the confidence interval band.
        xlabel: X-axis label.
        ylabel: Y-axis label.
        title: Optional plot title.

    Returns:
        Dictionary containing MSEs and coefficients statistics.
    """
    japanize_matplotlib.japanize()
    rng = np.random.default_rng(seed=0)

    x_values: np.ndarray = np.linspace(-4.0, 4.0, n_samples, dtype=float)
    y_clean: np.ndarray = 1.8 * x_values - 0.5
    y_noisy: np.ndarray = y_clean + rng.normal(scale=noise_scale, size=x_values.shape)

    outlier_idx = rng.choice(n_samples, size=outlier_count, replace=False)
    y_noisy[outlier_idx] += rng.normal(scale=outlier_scale, size=outlier_idx.shape)

    X: np.ndarray = x_values[:, np.newaxis]

    ols = LinearRegression()
    ols.fit(X, y_noisy)
    bayes = BayesianRidge(compute_score=True)
    bayes.fit(X, y_noisy)

    X_grid: np.ndarray = np.linspace(-6.0, 6.0, 200, dtype=float)[:, np.newaxis]
    ols_mean: np.ndarray = ols.predict(X_grid)
    bayes_mean, bayes_std = bayes.predict(X_grid, return_std=True)

    metrics = {
        "ols_mse": float(mean_squared_error(y_noisy, ols.predict(X))),
        "bayes_mse": float(mean_squared_error(y_noisy, bayes.predict(X))),
        "coef_mean": float(bayes.coef_[0]),
        "coef_std": float(np.sqrt(bayes.sigma_[0, 0])),
    }

    upper = bayes_mean + 1.96 * bayes_std
    lower = bayes_mean - 1.96 * bayes_std

    fig, ax = plt.subplots(figsize=(10, 5))
    ax.scatter(X, y_noisy, color="#ff7f0e", alpha=0.6, label=label_observations)
    ax.plot(X_grid, ols_mean, color="#1f77b4", linestyle="--", label=label_ols)
    ax.plot(X_grid, bayes_mean, color="#2ca02c", linewidth=2, label=label_bayes)
    ax.fill_between(
        X_grid.ravel(),
        lower,
        upper,
        color="#2ca02c",
        alpha=0.2,
        label=label_interval,
    )
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    if title:
        ax.set_title(title)
    ax.legend()
    fig.tight_layout()
    plt.show()

    return metrics

metrics = run_bayesian_linear_demo(
    label_observations="pengamatan",
    label_ols="OLS",
    label_bayes="Rata-rata Bayesian",
    label_interval="CI 95%",
    xlabel="masukan $",
    ylabel="keluaran $",
    title="Perbandingan regresi Bayesian dan OLS",
)
print(f"MSE OLS: {metrics['ols_mse']:.3f}")
print(f"MSE regresi Bayesian: {metrics['bayes_mse']:.3f}")
print(f"Rata-rata posterior koefisien: {metrics['coef_mean']:.3f}")
print(f"Standar deviasi koefisien: {metrics['coef_std']:.3f}")

Contoh berikut membandingkan mínimos kuadrat biasa dan regre… (diagram)

Cara membaca hasil #

OLS mudah terpengaruh oleh outlier, sedangkan regresi Bayesian menjaga prediksi rata-rata tetap stabil.
return_std=True memberikan simpangan baku prediktif sehingga interval kredibel dapat digambar dengan mudah.
Memeriksa varians posterior membantu mengidentifikasi koefisien mana yang masih memiliki ketidakpastian besar.

Referensi #

Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.
Murphy, K. P. (2012). Machine Learning: A Probabilistic Perspective. MIT Press.