Regresi linear

Diperbarui 2020-01-29 Baca 3 menit

Ringkasan

Regresi linear memodelkan hubungan linier antara masukan dan keluaran dan menjadi landasan untuk prediksi maupun interpretasi.
Metode kuadrat terkecil (ordinary least squares) menghitung koefisien dengan meminimalkan jumlah kuadrat residu sehingga menghasilkan solusi tertutup.
Koefisien kemiringan menunjukkan seberapa besar keluaran berubah ketika masukan bertambah satu satuan, sedangkan intercept memberi nilai harapan saat masukan bernilai nol.
Jika noise atau pencilan besar, kombinasikan standardisasi dan pendekatan robust agar praproses dan evaluasi tetap andal.

Intuisi #

Metode ini dipahami lewat asumsi dasarnya, karakteristik data, dan dampak pengaturan parameter terhadap generalisasi.

Penjelasan Rinci #

Formulasi matematis #

Model linear satu variabel ditulis sebagai

$$ y = w x + b. $$

Dengan meminimalkan jumlah kuadrat residu $\epsilon_i = y_i - (w x_i + b)$

$$ L(w, b) = \sum_{i=1}^{n} \big(y_i - (w x_i + b)\big)^2, $$

kita memperoleh solusi analitik

$$ w = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2}, \qquad b = \bar{y} - w \bar{x}, $$

dengan $\bar{x}$ dan $\bar{y}$ adalah rata-rata $x$ dan $y$. Ide yang sama berlaku untuk regresi multivariat menggunakan vektor dan matriks.

Eksperimen dengan Python #

Contoh berikut menyesuaikan garis regresi menggunakan scikit-learn dan menampilkan hasilnya. Kodenya sama seperti versi bahasa Jepang sehingga gambar yang dihasilkan konsisten.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

def plot_simple_linear_regression(n_samples: int = 100) -> None:
    """Plot a fitted linear regression model for synthetic data.

    Args:
        n_samples: Number of synthetic samples to generate.
    """
    japanize_matplotlib.japanize()
    rng = np.random.default_rng(seed=0)

    X: np.ndarray = np.linspace(-5.0, 5.0, n_samples, dtype=float)[:, np.newaxis]
    noise: np.ndarray = rng.normal(scale=2.0, size=n_samples)
    y: np.ndarray = 2.0 * X.ravel() + 1.0 + noise

    model = make_pipeline(StandardScaler(with_mean=False), LinearRegression())
    model.fit(X, y)
    y_pred: np.ndarray = model.predict(X)

    fig, ax = plt.subplots(figsize=(10, 5))
    ax.scatter(X, y, marker="x", label="Observed data", c="orange")
    ax.plot(X, y_pred, label="Regression fit")
    ax.set_xlabel("$x$")
    ax.set_ylabel("$y$")
    ax.legend()
    fig.tight_layout()
    plt.show()

plot_simple_linear_regression()

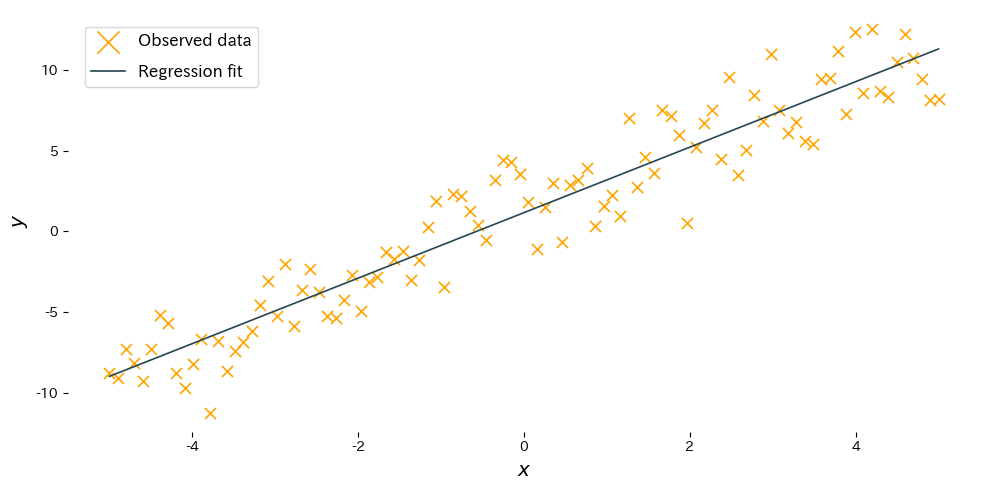
Kodenya sama seperti versi bahasa Jepang sehingga gambar yan… (diagram)

Membaca hasil #

Kemiringan $w$: menunjukkan seberapa besar keluaran naik atau turun ketika masukan bertambah satu satuan; estimasinya seharusnya mendekati nilai sebenarnya.
Intercept $b$: memberikan nilai harapan saat masukan bernilai 0 dan menggeser garis secara vertikal.
Menstandardisasi fitur dengan StandardScaler membantu stabilitas ketika skala masukan berbeda-beda.

Referensi #

Draper, N. R., & Smith, H. (1998). Applied Regression Analysis (3rd ed.). John Wiley & Sons.
Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning. Springer.