2.1.9
Regresi Partial Least Squares (PLS)
Ringkasan
- PLS mengekstrak faktor laten yang memaksimalkan kovarians antara prediktor dan target sebelum melakukan regresi.
- Berbeda dengan PCA, sumbu yang dipelajari memasukkan informasi target sehingga performa prediksi tetap terjaga saat dimensi dikurangi.
- Menyetel jumlah faktor laten menstabilkan model ketika terjadi multikolinearitas yang kuat.
- Melihat loading membantu mengidentifikasi kombinasi fitur yang paling berkaitan dengan target.
Intuisi #
Metode ini dipahami lewat asumsi dasarnya, karakteristik data, dan dampak pengaturan parameter terhadap generalisasi.
Penjelasan Rinci #
Formulasi matematis #
Dengan matriks prediktor \(\mathbf{X}\) dan vektor target \(\mathbf{y}\), PLS memperbarui skor laten \(\mathbf{t} = \mathbf{X} \mathbf{w}\) dan \(\mathbf{u} = \mathbf{y} c\) secara bergantian agar kovarians \(\mathbf{t}^\top \mathbf{u}\) maksimum. Pengulangan prosedur menghasilkan faktor laten tempat model linear
$$ \hat{y} = \mathbf{t} \boldsymbol{b} + b_0 $$dipasang. Jumlah faktor \(k\) biasanya dipilih melalui cross-validation.
Eksperimen dengan Python #
Berikut perbandingan kinerja PLS untuk berbagai jumlah faktor laten menggunakan dataset kebugaran Linnerud.
| |
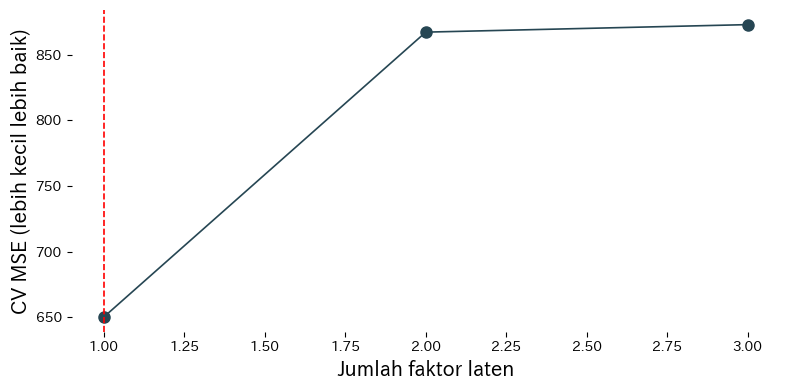
Cara membaca hasil #
- MSE hasil cross-validation menurun seiring penambahan faktor, mencapai minimum, lalu memburuk jika faktor ditambah terus.
- Meninjau
x_loadings_dany_loadings_menunjukkan fitur mana yang paling berkontribusi pada tiap faktor laten. - Menstandarkan masukan memastikan fitur dengan skala berbeda tetap berkontribusi secara seimbang.
Referensi #
- Wold, H. (1975). Soft Modelling by Latent Variables: The Non-Linear Iterative Partial Least Squares (NIPALS) Approach. Dalam Perspectives in Probability and Statistics. Academic Press.
- Geladi, P., & Kowalski, B. R. (1986). Partial Least-Squares Regression: A Tutorial. Analytica Chimica Acta, 185, 1–17.