Regresi Komponen Utama (PCR)

Diperbarui 2020-05-06 Baca 3 menit

Ringkasan

PCR menerapkan PCA untuk memampatkan fitur sebelum menjalankan regresi linear, sehingga mengurangi ketidakstabilan akibat multikolinearitas.
Komponen utama memprioritaskan arah dengan varians besar, menyaring sumbu yang didominasi noise sambil mempertahankan struktur informatif.
Menentukan jumlah komponen yang disimpan menyeimbangkan risiko overfitting dan biaya komputasi.
Praproses yang baik—standarisasi dan penanganan nilai hilang—menjadi fondasi akurasi dan interpretabilitas.

Intuisi #

Metode ini dipahami lewat asumsi dasarnya, karakteristik data, dan dampak pengaturan parameter terhadap generalisasi.

Penjelasan Rinci #

Formulasi matematis #

PCA diterapkan pada matriks rancangan $\mathbf{X}$ yang telah distandarkan, lalu $k$ autovektor teratas dipertahankan. Dengan skor komponen utama $\mathbf{Z} = \mathbf{X} \mathbf{W}_k$, model regresi

$$ y = \boldsymbol{\gamma}^\top \mathbf{Z} + b $$

dipelajari. Koefisien dalam ruang fitur asli dipulihkan melalui $\boldsymbol{\beta} = \mathbf{W}_k \boldsymbol{\gamma}$. Jumlah komponen $k$ dipilih menggunakan varian kumulatif atau cross-validation.

Eksperimen dengan Python #

Kami menghitung skor validasi silang PCR pada dataset diabetes sambil memvariasikan jumlah komponen.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_diabetes
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

def evaluate_pcr_components(
    cv_folds: int = 5,
    xlabel: str = "Number of components k",
    ylabel: str = "CV MSE (lower is better)",
    title: str | None = None,
    label_best: str = "best={k}",
) -> dict[str, float]:
    """Cross-validate PCR with varying component counts and plot the curve.

    Args:
        cv_folds: Number of folds for cross-validation.
        xlabel: Label for the component-count axis.
        ylabel: Label for the error axis.
        title: Optional title for the plot.
        label_best: Format string for highlighting the best component count.

    Returns:
        Dictionary containing the best component count and its CV score.
    """
    japanize_matplotlib.japanize()
    X, y = load_diabetes(return_X_y=True)

    def build_pcr(n_components: int) -> Pipeline:
        return Pipeline([
            ("scale", StandardScaler()),
            ("pca", PCA(n_components=n_components, random_state=0)),
            ("reg", LinearRegression()),
        ])

    components = np.arange(1, X.shape[1] + 1)
    cv_scores = []
    for k in components:
        model = build_pcr(int(k))
        score = cross_val_score(
            model,
            X,
            y,
            cv=cv_folds,
            scoring="neg_mean_squared_error",
        )
        cv_scores.append(score.mean())

    cv_scores_arr = np.array(cv_scores)
    best_idx = int(np.argmax(cv_scores_arr))
    best_k = int(components[best_idx])
    best_mse = float(-cv_scores_arr[best_idx])

    best_model = build_pcr(best_k).fit(X, y)
    explained = best_model["pca"].explained_variance_ratio_

    fig, ax = plt.subplots(figsize=(8, 4))
    ax.plot(components, -cv_scores_arr, marker="o")
    ax.axvline(best_k, color="red", linestyle="--", label=label_best.format(k=best_k))
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    if title:
        ax.set_title(title)
    ax.legend()
    fig.tight_layout()
    plt.show()

    return {
        "best_k": best_k,
        "best_mse": best_mse,
        "explained_variance_ratio": explained,
    }

metrics = evaluate_pcr_components(
    xlabel="Jumlah komponen k",
    ylabel="MSE CV (semakin kecil semakin baik)",
    title="PCR vs jumlah komponen",
    label_best="k terbaik={k}",
)
print(f"Jumlah komponen terbaik: {metrics['best_k']}")
print(f"MSE CV terbaik: {metrics['best_mse']:.3f}")
print("Rasio varians yang dijelaskan:", metrics['explained_variance_ratio'])

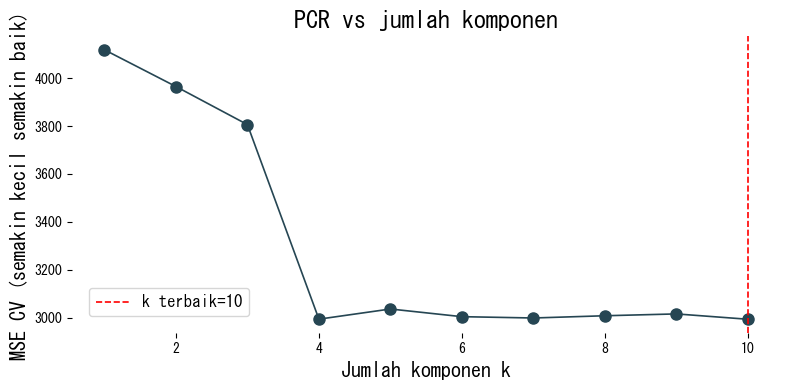
Kami menghitung skor validasi silang PCR pada dataset diabet… (diagram)

Cara membaca hasil #

Semakin banyak komponen, kecocokan terhadap data latih meningkat, tetapi MSE validasi silang mencapai minimum pada jumlah menengah.
Rasio varians yang dijelaskan memperlihatkan seberapa besar variabilitas yang ditangkap tiap komponen.
Loading komponen menunjukkan fitur asli mana yang paling berkontribusi pada setiap arah utama.

Referensi #

Jolliffe, I. T. (2002). Principal Component Analysis (2nd ed.). Springer.
Massy, W. F. (1965). Principal Components Regression in Exploratory Statistical Research. Journal of the American Statistical Association, 60(309), 234–256.