2.1.7
Regresi Kuantil
Ringkasan
- Regresi kuantil mengestimasi kuantil arbitrer—misalnya median atau persentil ke-10—secara langsung alih-alih hanya rata-rata.
- Dengan meminimalkan loss pinball, model menjadi tahan terhadap outlier dan mampu menangani noise yang tidak simetris.
- Model untuk berbagai kuantil dapat dilatih secara terpisah dan digabungkan menjadi interval prediksi.
- Penyetaraan skala fitur dan regularisasi membantu menstabilkan konvergensi serta menjaga kemampuan generalisasi.
Intuisi #
Metode ini dipahami lewat asumsi dasarnya, karakteristik data, dan dampak pengaturan parameter terhadap generalisasi.
Penjelasan Rinci #
Formulasi matematis #
Dengan residual \(r = y - \hat{y}\) dan level kuantil \(\tau \in (0, 1)\), loss pinball didefinisikan sebagai
$$ L_\tau(r) = \begin{cases} \tau r & (r \ge 0) \\ (\tau - 1) r & (r < 0) \end{cases} $$Meminimalkan loss ini menghasilkan prediktor linear untuk kuantil \(\tau\). Ketika \(\tau = 0.5\) kita memperoleh median, identik dengan regresi deviasi absolut.
Eksperimen dengan Python #
Kita menggunakan QuantileRegressor untuk mengestimasi kuantil 0.1, 0.5, dan 0.9, lalu membandingkannya dengan mínimos kuadrat biasa.
| |
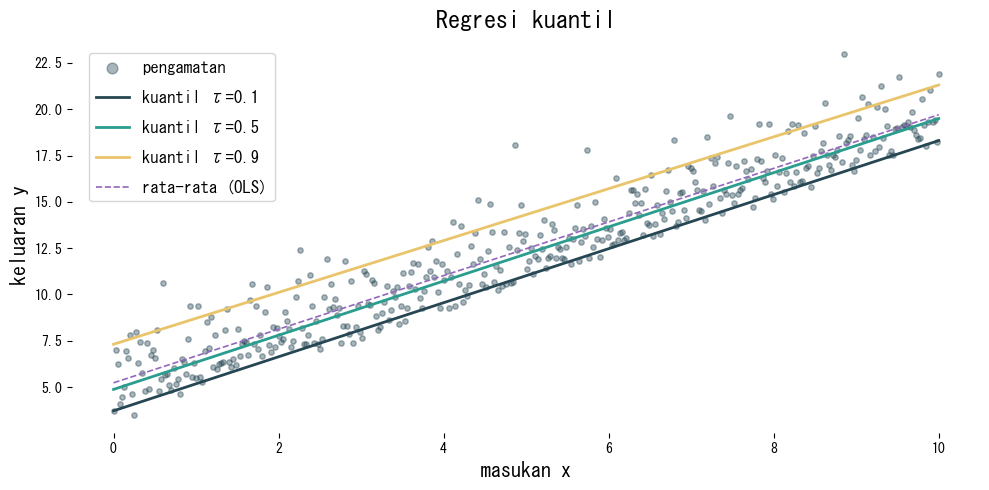
Cara membaca hasil #
- Setiap kuantil menghasilkan garis berbeda yang menggambarkan sebaran vertikal data.
- Dibandingkan model rata-rata (OLS), regresi kuantil menyesuaikan diri terhadap noise yang miring.
- Menggabungkan beberapa kuantil menghasilkan interval prediksi yang menyampaikan ketidakpastian penting untuk pengambilan keputusan.
Referensi #
- Koenker, R., & Bassett, G. (1978). Regression Quantiles. Econometrica, 46(1), 33–50.
- Koenker, R. (2005). Quantile Regression. Cambridge University Press.