Weighted Least Squares (WLS)

Diperbarui 2020-06-17 Baca 3 menit

Ringkasan

WLS memberikan bobot khusus pada tiap observasi sehingga pengukuran yang lebih dapat dipercaya memiliki pengaruh lebih besar pada garis regresi.
Mengalikan error kuadrat dengan bobot membuat observasi ber-varians tinggi kurang berpengaruh dan menjaga estimasi tetap dekat dengan data yang andal.
WLS dapat dijalankan menggunakan LinearRegression di scikit-learn dengan menyediakan sample_weight.
Bobot dapat berasal dari varians yang diketahui, analisis residual, atau pengetahuan domain; perancangannya sangat krusial.

Intuisi #

Metode ini dipahami lewat asumsi dasarnya, karakteristik data, dan dampak pengaturan parameter terhadap generalisasi.

Penjelasan Rinci #

Formulasi matematis #

Dengan bobot positif $w_i$ kita meminimalkan

$$ L(\boldsymbol\beta, b) = \sum_{i=1}^{n} w_i \left(y_i - (\boldsymbol\beta^\top \mathbf{x}_i + b)\right)^2. $$

Pilihan idealnya adalah $w_i \propto 1/\sigma_i^2$ (kebalikan varians) sehingga observasi yang presisi memiliki pengaruh lebih besar.

Eksperimen dengan Python #

Kami membandingkan OLS dan WLS pada data dengan tingkat noise berbeda di setiap wilayah.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression

def run_weighted_vs_ols(
    n_samples: int = 200,
    threshold: float = 5.0,
    low_noise: float = 0.5,
    high_noise: float = 2.5,
    xlabel: str = "input $",
    ylabel: str = "output $",
    label_scatter: str = "observations (color=noise)",
    label_truth: str = "true line",
    label_ols: str = "OLS",
    label_wls: str = "WLS",
    title: str | None = None,
) -> dict[str, float]:
    """Compare OLS and weighted least squares on heteroscedastic data.

    Args:
        n_samples: Number of evenly spaced samples to generate.
        threshold: Breakpoint separating low- and high-noise regions.
        low_noise: Noise scale for the lower region.
        high_noise: Noise scale for the higher region.
        xlabel: Label for the x-axis.
        ylabel: Label for the y-axis.
        label_scatter: Legend label for the colored scatter plot.
        label_truth: Legend label for the ground-truth line.
        label_ols: Legend label for the OLS fit.
        label_wls: Legend label for the WLS fit.
        title: Optional title for the plot.

    Returns:
        Dictionary with slopes and intercepts of both fits.
    """
    japanize_matplotlib.japanize()
    rng = np.random.default_rng(7)

    X_vals: np.ndarray = np.linspace(0.0, 10.0, n_samples, dtype=float)
    true_y: np.ndarray = 1.2 * X_vals + 3.0

    noise_scale = np.where(X_vals < threshold, low_noise, high_noise)
    y_noisy = true_y + rng.normal(scale=noise_scale)

    weights = 1.0 / (noise_scale**2)
    X = X_vals[:, np.newaxis]

    ols = LinearRegression()
    ols.fit(X, y_noisy)

    wls = LinearRegression()
    wls.fit(X, y_noisy, sample_weight=weights)

    grid = np.linspace(0.0, 10.0, 200, dtype=float)[:, np.newaxis]
    ols_pred = ols.predict(grid)
    wls_pred = wls.predict(grid)

    fig, ax = plt.subplots(figsize=(10, 5))
    scatter = ax.scatter(
        X,
        y_noisy,
        c=noise_scale,
        cmap="coolwarm",
        s=25,
        label=label_scatter,
    )
    ax.plot(grid, 1.2 * grid.ravel() + 3.0, color="#2ca02c", label=label_truth)
    ax.plot(grid, ols_pred, color="#1f77b4", linestyle="--", linewidth=2, label=label_ols)
    ax.plot(grid, wls_pred, color="#d62728", linewidth=2, label=label_wls)
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    if title:
        ax.set_title(title)
    ax.legend()
    fig.tight_layout()
    plt.show()

    return {
        "ols_slope": float(ols.coef_[0]),
        "ols_intercept": float(ols.intercept_),
        "wls_slope": float(wls.coef_[0]),
        "wls_intercept": float(wls.intercept_),
    }

metrics = run_weighted_vs_ols(
    xlabel="masukan $",
    ylabel="keluaran $",
    label_scatter="observasi (warna=noise)",
    label_truth="garis sebenarnya",
    label_ols="OLS",
    label_wls="WLS",
    title="Perbandingan OLS dan WLS",
)
print(f"Kemiringan OLS: {metrics['ols_slope']:.3f}, intercept: {metrics['ols_intercept']:.3f}")
print(f"Kemiringan WLS: {metrics['wls_slope']:.3f}, intercept: {metrics['wls_intercept']:.3f}")

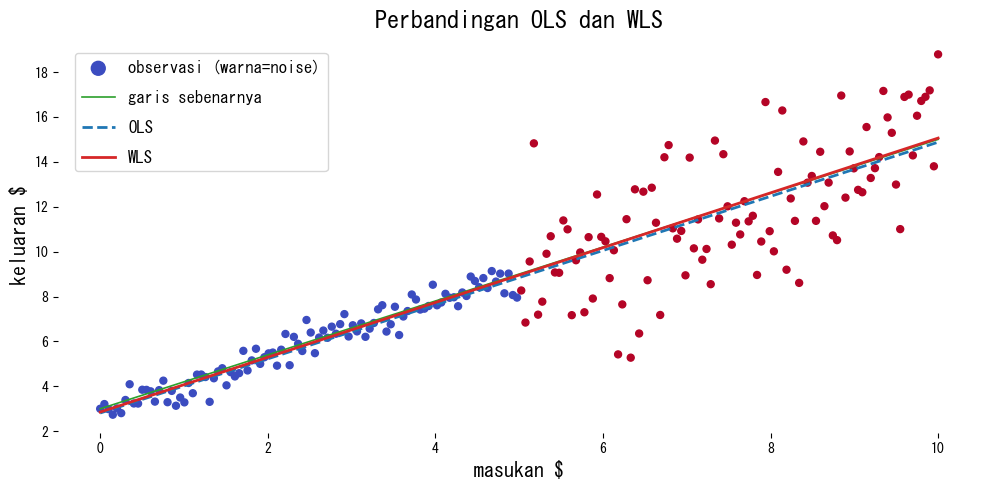
Kami membandingkan OLS dan WLS pada data dengan tingkat nois… (diagram)

Cara membaca hasil #

Pemberian bobot menarik garis hasil fitting ke wilayah dengan noise rendah sehingga mendekati garis sebenarnya.
OLS terdistorsi oleh wilayah dengan noise tinggi dan cenderung meremehkan kemiringan.
Kinerja sangat bergantung pada pemilihan bobot yang tepat; diagnosa dan intuisi domain sangat membantu.

Referensi #

Carroll, R. J., & Ruppert, D. (1988). Transformation and Weighting in Regression. Chapman & Hall.
Seber, G. A. F., & Lee, A. J. (2012). Linear Regression Analysis (2nd ed.). Wiley.