Pohon keputusan (regresi)

2.3.2

Pohon keputusan (regresi)

Diperbarui 2025-11-05 Baca 3 menit
Ringkasan
  • Pohon regresi menangkap hubungan nonlinier dengan memecah ruang fitur secara rekursif hingga setiap daun dapat diringkas dengan satu nilai konstan.
  • Kualitas split diukur lewat penurunan mean squared error (MSE) pada node anak; semakin besar penurunan, semakin baik pertanyaannya.
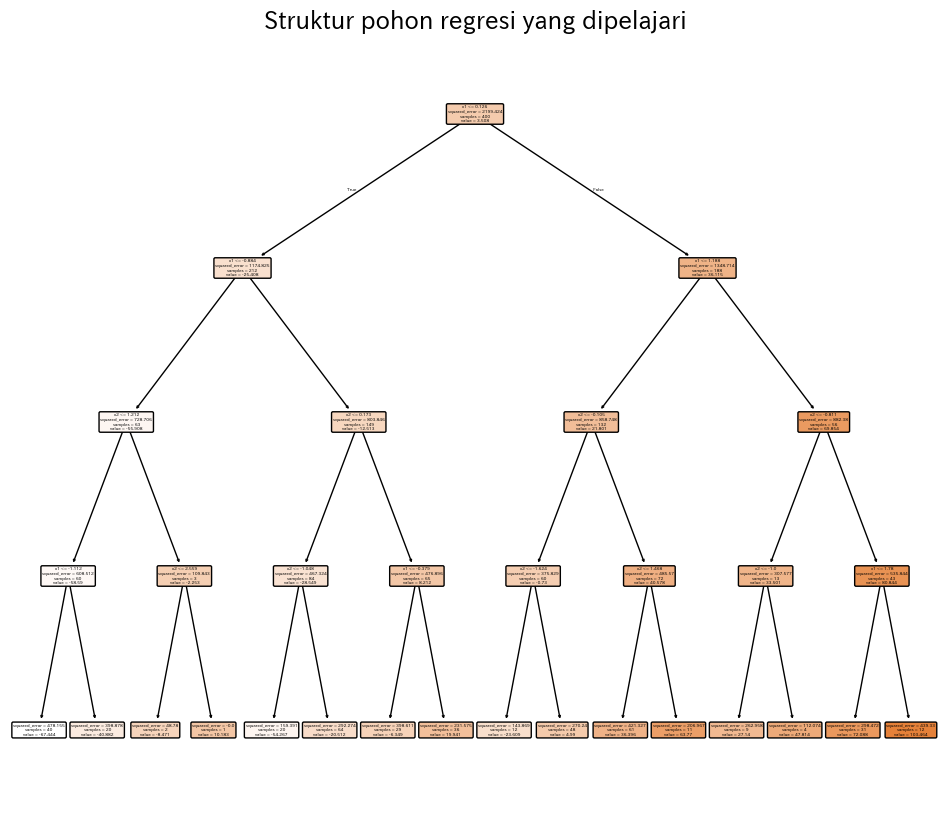
  • Parameter max_depth, min_samples_leaf, dan ccp_alpha membantu menjaga keseimbangan antara ketelitian dan interpretabilitas serta menekan overfitting.
  • Scatter plot, peta kontur, dan visualisasi pohon memudahkan kita menjelaskan area mana yang berbagi prediksi sama.

Intuisi #

Metode ini dipahami lewat asumsi dasarnya, karakteristik data, dan dampak pengaturan parameter terhadap generalisasi.

Penjelasan Rinci #

1. Gambaran umum #

Serupa dengan klasifikasi, pohon regresi menanyakan pertanyaan sederhana tentang fitur, namun targetnya kini bersifat kontinu. Setiap daun mengeluarkan rata-rata sampel yang masuk, sehingga fungsi yang dihasilkan bersifat konstan per segmen. Pohon yang dalam menangkap detail halus, sedangkan pohon dangkal menjaga tren global.

2. Kriteria pemisahan (reduksi varians) #

Untuk node (t) dengan (n_t) sampel dan rata-rata (\bar{y}_t), impuritasnya didefinisikan sebagai

$$ \mathrm{MSE}(t) = \frac{1}{n_t} \sum_{i \in t} (y_i - \bar{y}_t)^2. $$

Jika (t) dibagi menggunakan fitur (x_j) dan ambang (s), keuntungan yang diperoleh adalah

$$ \Delta = \mathrm{MSE}(t) - \frac{n_L}{n_t} \mathrm{MSE}(t_L) - \frac{n_R}{n_t} \mathrm{MSE}(t_R). $$

Split terbaik adalah yang memaksimalkan (\Delta); ketika tidak ada split yang memberikan keuntungan positif, node berubah menjadi daun.

3. Contoh Python #

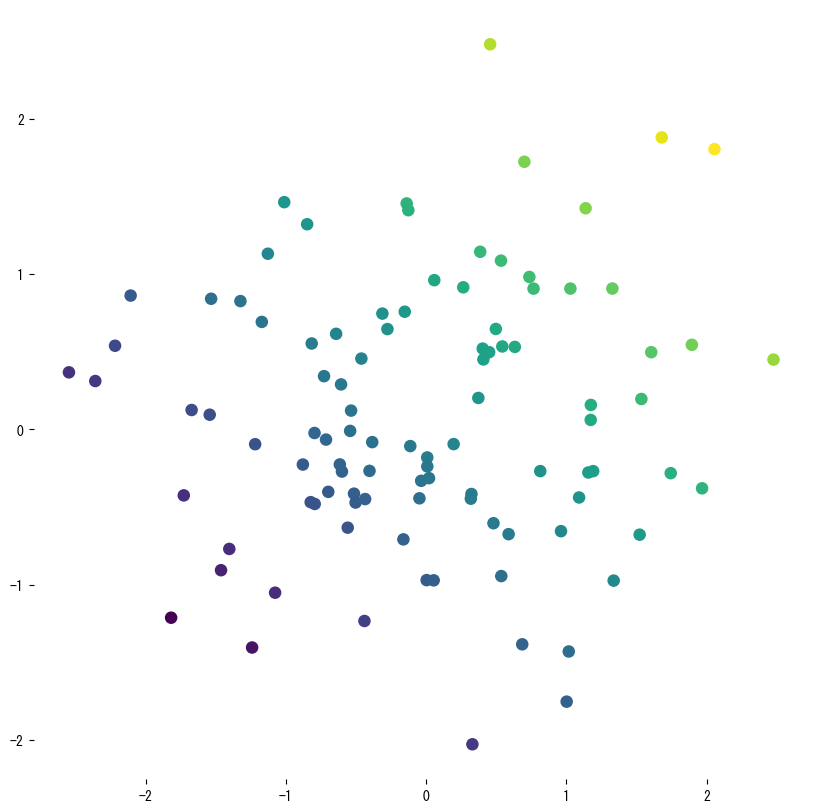
Cuplikan pertama melatih pohon dangkal pada sampel sinusoid yang diberi derau untuk menunjukkan bentuk fungsi yang konstan per segmen. Eksperimen kedua menggunakan dua fitur, menghitung (R^2), RMSE, MAE, dan menggambarkan permukaan prediksi serta struktur pohonnya.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor, plot_tree
from sklearn.datasets import make_regression
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error

rng = np.random.default_rng(42)
X1 = np.sort(5 * rng.random((120, 1)), axis=0)
y1_true = np.sin(X1).ravel()
y1 = y1_true + rng.normal(scale=0.2, size=X1.shape[0])

reg1 = DecisionTreeRegressor(max_depth=3, random_state=0).fit(X1, y1)
y1_pred = reg1.predict(X1)

plt.figure(figsize=(8, 4))
plt.scatter(X1, y1, s=15, c="gray", label="observasi")
plt.plot(X1, y1_true, lw=2, label="sinyal asli")
plt.step(X1.ravel(), y1_pred, where="mid", lw=2, label="prediksi pohon")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Pohon regresi menghasilkan fungsi konstan per segmen")
plt.legend()
plt.grid(alpha=0.3)
plt.show()

Pohon regresi pada sinyal sinus

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

X, y = make_regression(n_samples=400, n_features=2, noise=15.0, random_state=777)
reg = DecisionTreeRegressor(max_depth=4, random_state=0).fit(X, y)

r2 = r2_score(y, reg.predict(X))
rmse = mean_squared_error(y, reg.predict(X), squared=False)
mae = mean_absolute_error(y, reg.predict(X))
print(f"R2={r2:.3f}  RMSE={rmse:.2f}  MAE={mae:.2f}")

x_min, x_max = X[:, 0].min()-1, X[:, 0].max()+1
y_min, y_max = X[:, 1].min()-1, X[:, 1].max()+1
xx, yy = np.meshgrid(
    np.linspace(x_min, x_max, 150),
    np.linspace(y_min, y_max, 150),
)
zz = reg.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)

plt.figure(figsize=(7, 6))
cs = plt.contourf(xx, yy, zz, levels=15, cmap="viridis", alpha=0.8)
plt.colorbar(cs, label="prediksi")
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="viridis", s=20, edgecolor="k", alpha=0.7)
plt.xlabel("x1")
plt.ylabel("x2")
plt.title("Permukaan prediksi pohon regresi")
plt.show()

Permukaan prediksi pohon regresi

1
2
3
4
5
6
7
8
9

plt.figure(figsize=(12, 10))
plot_tree(
    reg,
    filled=True,
    feature_names=["x1", "x2"],
    rounded=True,
)
plt.title("Struktur pohon regresi yang dipelajari")
plt.show()

Struktur pohon yang divisualisasikan

4. Referensi #

  • Breiman, L., Friedman, J. H., Olshen, R. A., & Stone, C. J. (1984). Classification and Regression Trees. Wadsworth.
  • scikit-learn developers. (2024). Decision Trees. https://scikit-learn.org/stable/modules/tree.html