Parameter pohon

2.3.3

Parameter pohon

Diperbarui 2025-11-05 Baca 2 menit
Ringkasan
  • Pohon keputusan memiliki banyak pengaturan—kedalaman, jumlah sampel minimum per split/leaf, pruning, dan bobot kelas—yang menentukan kapasitas serta kemudahan interpretasi.
  • max_depth dan min_samples_leaf membatasi seberapa rinci aturan yang terbentuk, sedangkan ccp_alpha (cost-complexity pruning) menghapus cabang yang kontribusinya kecil.
  • Memilih kriteria yang tepat (squared_error, absolute_error, friedman_mse, dll.) mengubah sensitivitas pohon terhadap pencilan.
  • Visualisasi permukaan prediksi dan struktur pohon mempermudah penjelasan mengapa kombinasi hiperparameter tertentu bekerja paling baik.

Intuisi #

Metode ini dipahami lewat asumsi dasarnya, karakteristik data, dan dampak pengaturan parameter terhadap generalisasi.

Penjelasan Rinci #

1. Gambaran umum #

Jika tidak dibatasi, pohon akan terus membelah hingga setiap daun murni—cenderung overfitting. Hiperparameter berperan sebagai regularisasi: kedalaman menjaga pohon tetap dangkal, batas sampel minimum mencegah daun kecil, dan pruning merapikan cabang yang tidak sepadan dengan biayanya.

2. Gain impunitas dan pruning cost-complexity #

Untuk node induk (P) dengan anak (L) dan (R), penurunan impuritas adalah

$$ \Delta I = I(P) - \frac{|L|}{|P|} I(L) - \frac{|R|}{|P|} I(R), $$

di mana (I(\cdot)) bisa berupa Gini, entropi, MSE, atau MAE. Hanya split dengan (\Delta I > 0) yang dipertahankan.

Penyeleksian pohon melalui cost-complexity menilai (T) dengan

$$ R_\alpha(T) = R(T) + \alpha |T|, $$

dengan (R(T)) sebagai loss pelatihan, (|T|) jumlah daun, dan (\alpha \ge 0) penalti ukuran. Semakin besar (\alpha), semakin sederhana pohonnya.

3. Eksperimen Python #

Kode berikut melatih beberapa DecisionTreeRegressor pada data sintetis dan memperlihatkan bagaimana variasi parameter memengaruhi skor (R^2) train/test.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
from sklearn.datasets import make_regression
from sklearn.metrics import r2_score

X, y = make_regression(
    n_samples=500,
    n_features=2,
    noise=0.2,
    random_state=42,
)
Xtr, Xte, ytr, yte = train_test_split(X, y, test_size=0.3, random_state=0)

def evaluate(params):
    model = DecisionTreeRegressor(random_state=0, **params).fit(Xtr, ytr)
    r2_train = r2_score(ytr, model.predict(Xtr))
    r2_test = r2_score(yte, model.predict(Xte))
    print(f"{params}: train R2={r2_train:.3f}, test R2={r2_test:.3f}")

evaluate({"max_depth": 3})
evaluate({"max_depth": 10})
evaluate({"max_depth": 5, "min_samples_leaf": 5})
evaluate({"max_depth": 5, "ccp_alpha": 0.01})

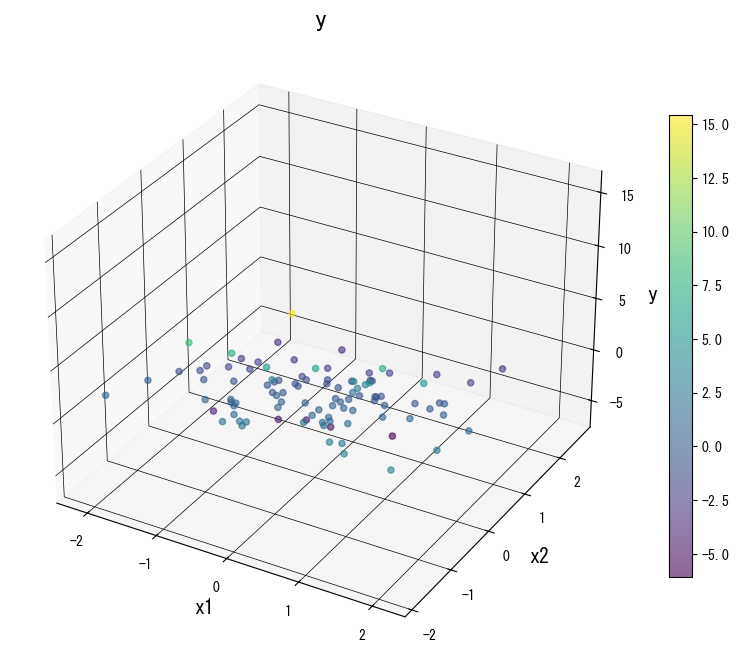
Gunakan galeri berikut sebagai referensi visual saat menala pohon:

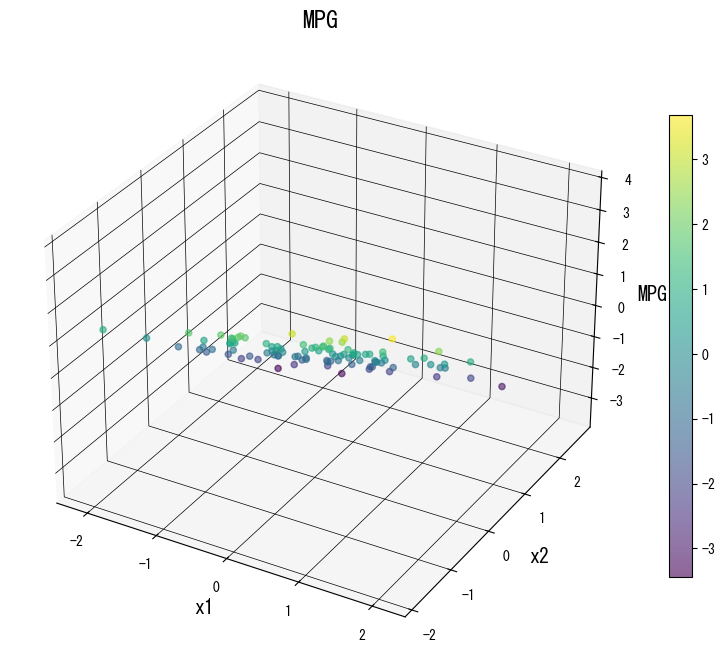
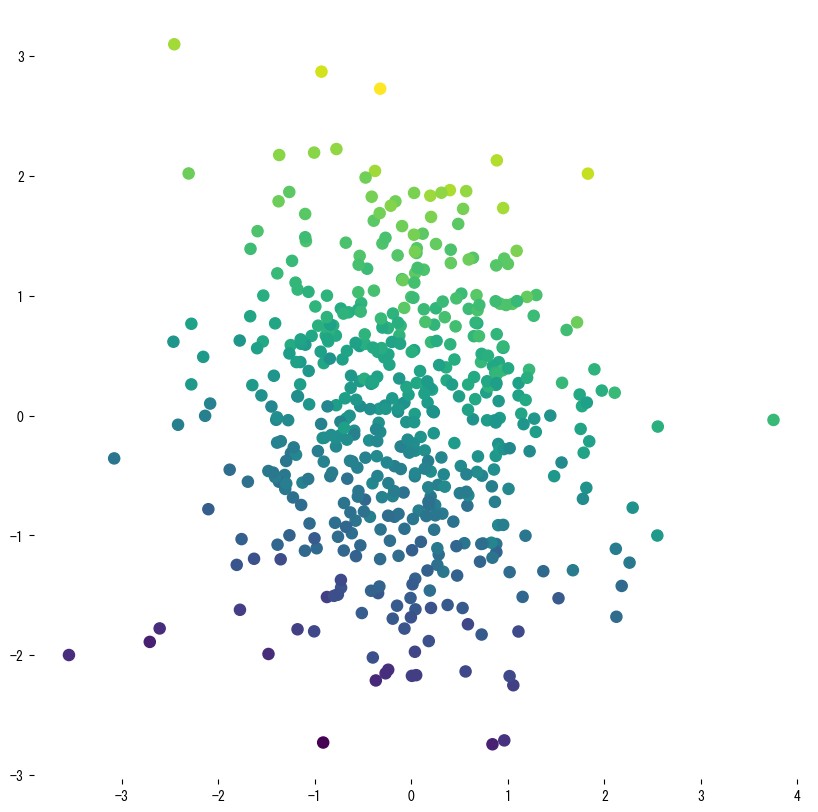
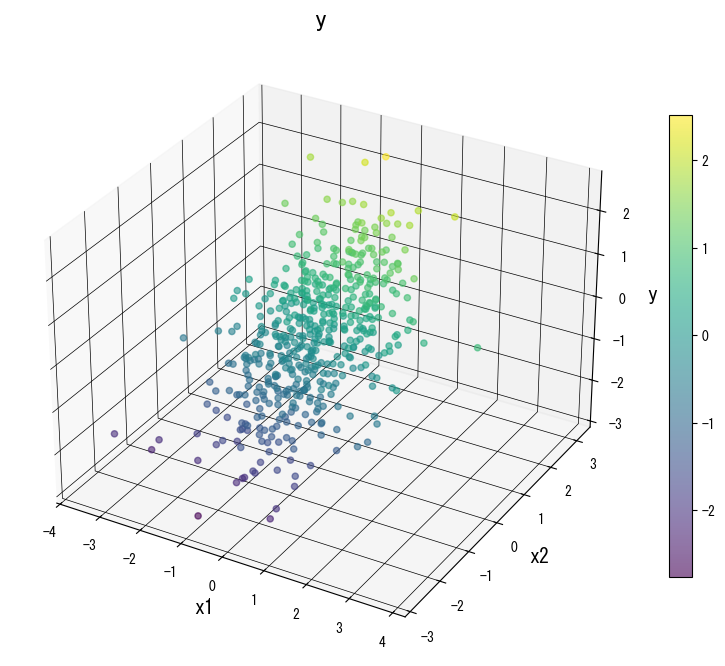
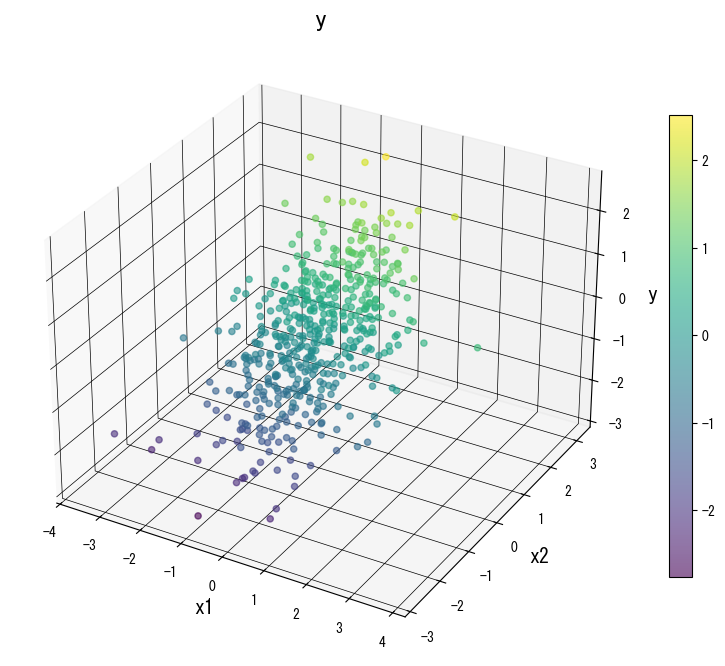
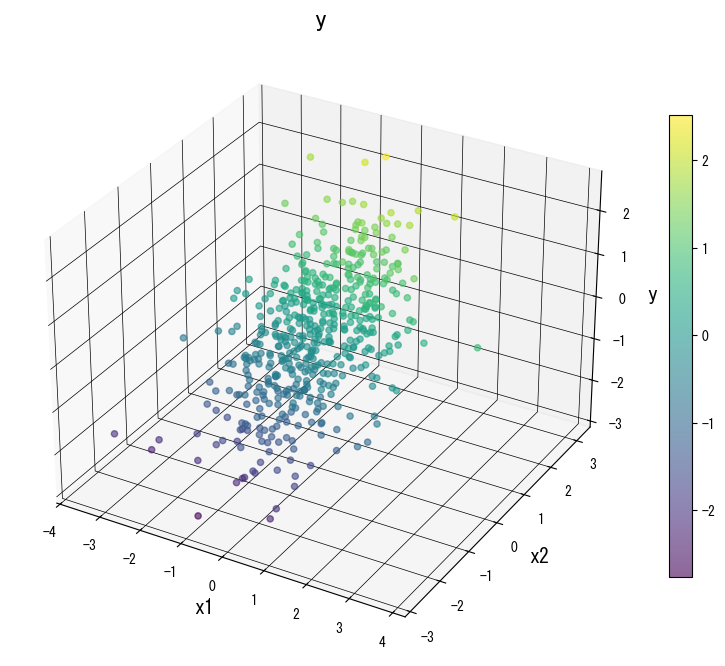
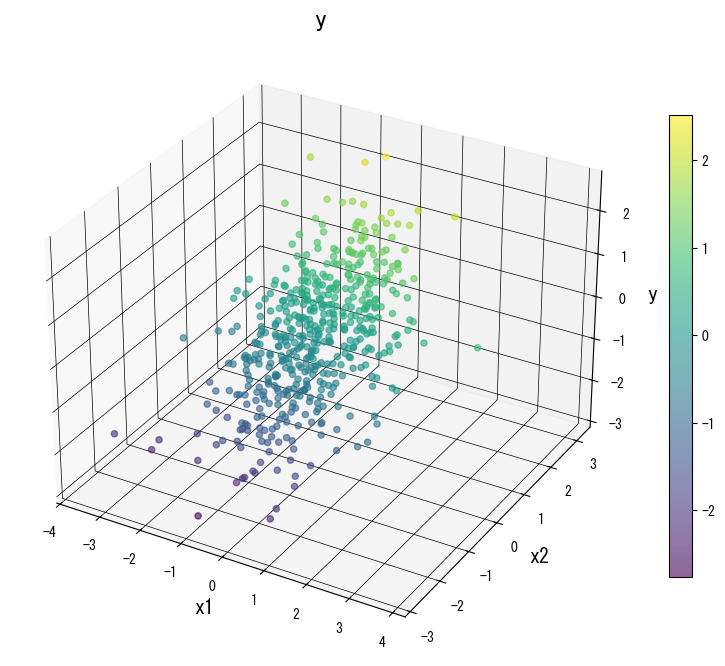
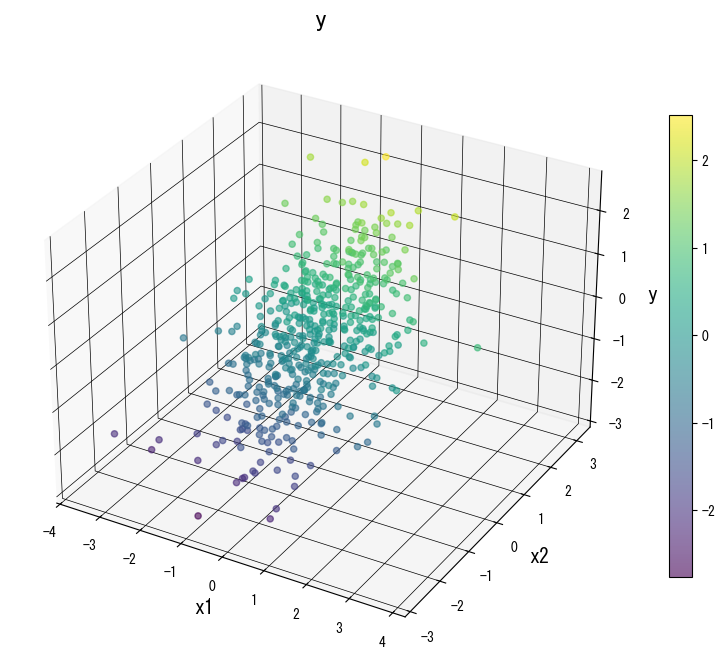
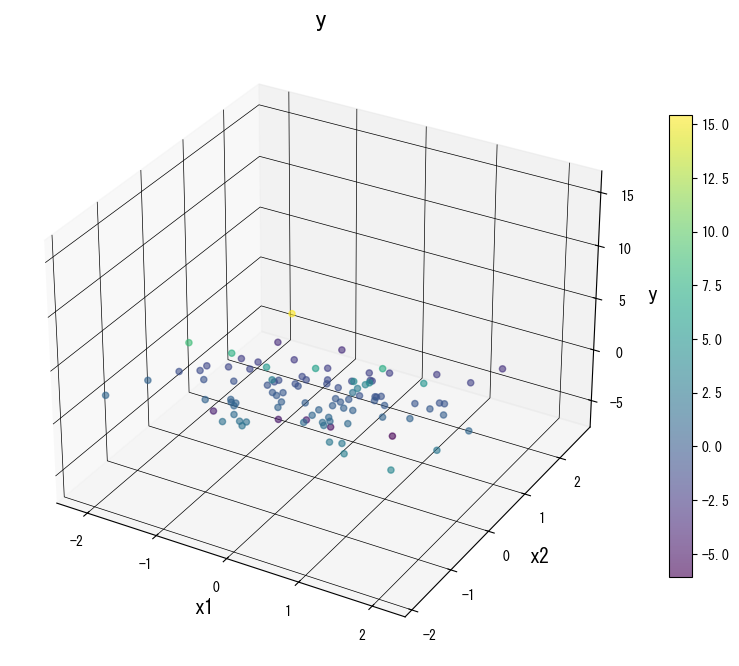
Pohon dasar dengan max_depth=3 Sebaran data dan pemodelan awal Permukaan 3D dari pemodelan awal Pohon lebih dalam (max_depth=10) Efek min_samples_leaf=20 Pohon hasil pruning ccp_alpha=0.4 Batas jumlah daun max_leaf_nodes=5 Kriteria absolute_error saat ada pencilan Kriteria squared_error saat ada pencilan

4. Referensi #

  • Breiman, L., Friedman, J. H., Olshen, R. A., & Stone, C. J. (1984). Classification and Regression Trees. Wadsworth.
  • Breiman, L., & Friedman, J. H. (1991). Cost-Complexity Pruning. Dalam Classification and Regression Trees. Chapman & Hall.
  • scikit-learn developers. (2024). Decision Trees. https://scikit-learn.org/stable/modules/tree.html