Kullback-Leibler Divergence
KL Divergence
Kullback-Leibler Divergence adalah ukuran numerik yang menunjukkan perbedaan antara dua distribusi probabilitas. Ini dapat dihitung dengan mengurangkan entropi informasi dari entropi silang.
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from scipy.special import kl_div
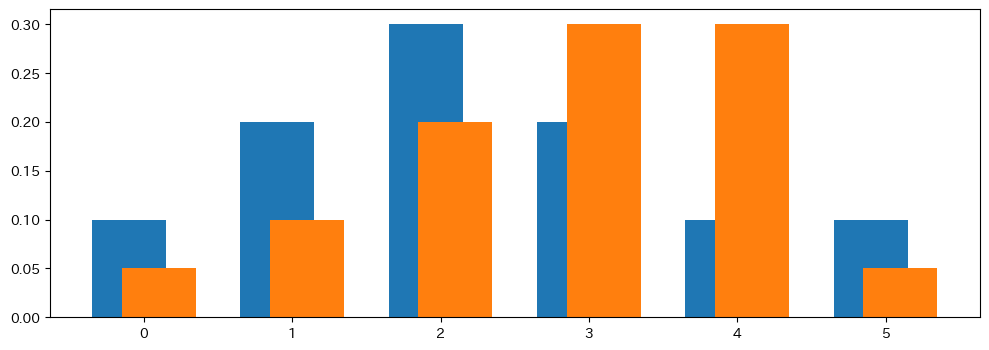
Dua Distribusi
plt.figure(figsize=(12, 4))
a = np.array([0.1, 0.2, 0.3, 0.2, 0.1, 0.1])
b = np.array([0.05, 0.1, 0.2, 0.3, 0.3, 0.05])
plt.bar(np.arange(a.shape[0]) - 0.1, a, width=0.5)
plt.bar(np.arange(b.shape[0]) + 0.1, b, width=0.5)
KLD
def kld(dist1, dist2):
"""KL Divergence"""
assert dist1.shape == dist2.shape, "Distribusi probabilitas 1 dan 2 harus memiliki panjang yang sama"
assert all(dist1) != 0 and all(dist2) != 0, "Distribusi probabilitas tidak boleh mengandung nilai 0"
dist1 = dist1 / np.sum(dist1)
dist2 = dist2 / np.sum(dist2)
return sum([p1 * np.log2(p1 / p2) for p1, p2 in zip(dist1, dist2)])
print(f"Jika distribusi sama, KLD harus 0 → {kld(a, a)}")
print(f"Jika distribusi berbeda, KLD harus lebih besar dari 0 → {kld(a, b)}")
print(f"Jika distribusi berbeda, KLD harus lebih besar dari 0, tetapi mungkin berbeda dari kld(a, b) → {kld(b, a)}")
Jika distribusi sama, KLD harus 0 → 0.0
Jika distribusi berbeda, KLD harus lebih besar dari 0 → 0.3
Jika distribusi berbeda, KLD harus lebih besar dari 0, tetapi mungkin berbeda dari kld(a, b) → 0.3339850002884623
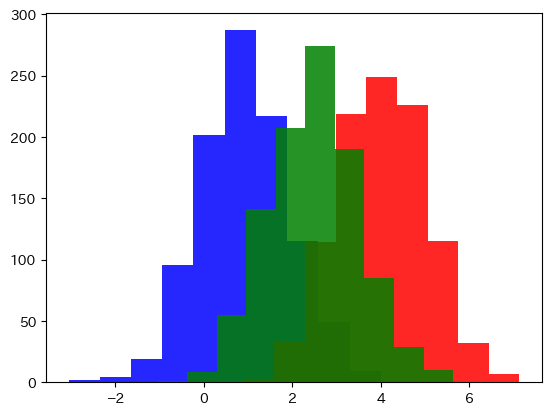
Pengenalan Jensen–Shannon Divergence
plt.hist(np.random.normal(1, 1, 1000), alpha=0.85, color="blue")
plt.hist(np.random.normal(4, 1, 1000), alpha=0.85, color="red")
plt.hist(np.random.normal(2.5, 1, 1000), alpha=0.85, color="green")
plt.show()