Koefisien korelasi
Koefisien korelasi mengukur kekuatan hubungan linier antara dua data atau variabel acak. Ini adalah indikator yang memungkinkan kita untuk memeriksa apakah ada perubahan tren bentuk linier antara dua variabel, yang dapat dinyatakan dalam persamaan berikut.
$ \frac{\Sigma_{i=1}^N (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\Sigma_{i=1}^N(x_i - \bar{x})^2 \Sigma_{i=1}^N(y_i - \bar{y})^2 }} $
Ini memiliki sifat-sifat berikut
- -1 sampai kurang dari 1
- Jika koefisien korelasi mendekati 1, $x$ meningkat → $y$ juga meningkat
- Nilai koefisien korelasi tidak berubah ketika $x, y$ dikalikan dengan angka yang rendah
Hitung koefisien korelasi antara dua kolom numerik
import numpy as np
np.random.seed(777) # untuk memperbaiki angka acak
import matplotlib.pyplot as plt
import numpy as np
x = [xi + np.random.rand() for xi in np.linspace(0, 100, 40)]
y = [yi + np.random.rand() for yi in np.linspace(1, 50, 40)]
plt.figure(figsize=(5, 5))
plt.scatter(x, y)
plt.show()
coef = np.corrcoef(x, y)
print(coef)
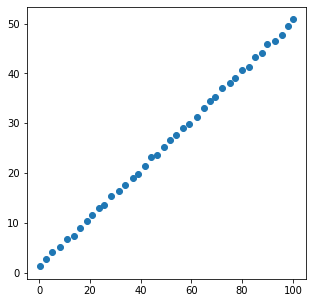
[[1. 0.99979848]
[0.99979848 1. ]]
Secara kolektif menghitung koefisien korelasi antara beberapa variabel
import seaborn as sns
df = sns.load_dataset("iris")
df.head()
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
Periksa KORELASI KORELASI antara semua variabel
Dengan menggunakan dataset iris mata, mari kita lihat korelasi antar variabel.
df.corr().style.background_gradient(cmap="YlOrRd")
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| sepal_length | 1.000000 | -0.117570 | 0.871754 | 0.817941 |
| sepal_width | -0.117570 | 1.000000 | -0.428440 | -0.366126 |
| petal_length | 0.871754 | -0.428440 | 1.000000 | 0.962865 |
| petal_width | 0.817941 | -0.366126 | 0.962865 | 1.000000 |
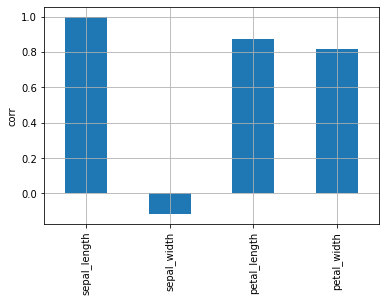
Dalam peta panas, sulit untuk melihat di mana korelasi tertinggi. Periksa diagram batang untuk melihat variabel mana yang memiliki korelasi tertinggi dengan sepal_length.
df.corr()["sepal_length"].plot.bar(grid=True, ylabel="corr")
<AxesSubplot:ylabel='corr'>
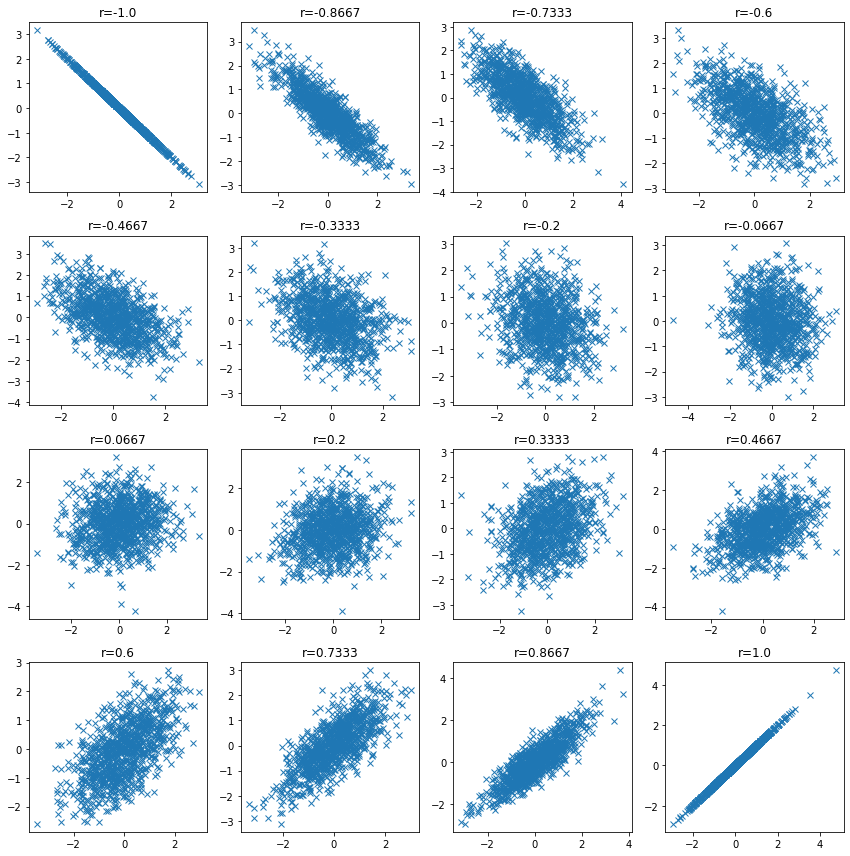
Ketika koefisien korelasi rendah
Periksa distribusi data ketika koefisien korelasi rendah dan konfirmasikan bahwa koefisien korelasi mungkin rendah bahkan ketika ada hubungan antar variabel.
n_samples = 1000
plt.figure(figsize=(12, 12))
for i, ci in enumerate(np.linspace(-1, 1, 16)):
ci = np.round(ci, 4)
mean = np.array([0, 0])
cov = np.array([[1, ci], [ci, 1]])
v1, v2 = np.random.multivariate_normal(mean, cov, size=n_samples).T
plt.subplot(4, 4, i + 1)
plt.plot(v1, v2, "x")
plt.title(f"r={ci}")
plt.tight_layout()
plt.show()
Dalam beberapa kasus, ada hubungan antara variabel bahkan jika koefisien korelasinya rendah. Kita akan mencoba membuat contoh seperti itu, meskipun sederhana.
import japanize_matplotlib
from sklearn import datasets
japanize_matplotlib.japanize()
n_samples = 1000
circle, _ = datasets.make_circles(n_samples=n_samples, factor=0.1, noise=0.05)
moon, _ = datasets.make_moons(n_samples=n_samples, noise=0.05)
corr_circle = np.round(np.corrcoef(circle[:, 0], circle[:, 1])[1, 0], 4)
plt.title(f"koefisien korelasi={corr_circle}", fontsize=23)
plt.scatter(circle[:, 0], circle[:, 1])
plt.show()
corr_moon = np.round(np.corrcoef(moon[:, 0], moon[:, 1])[1, 0], 4)
plt.title(f"koefisien korelasi={corr_moon}", fontsize=23)
plt.scatter(moon[:, 0], moon[:, 1])
plt.show()
