Koefisien determinasi

Diperbarui 2020-02-12 Baca 4 menit

Ringkasan

Koefisien determinasiの概要を押さえ、評価対象と読み取り方を整理します。
Python 3.13 のコード例で算出・可視化し、手順と実務での確認ポイントを確認します。
図表や補助指標を組み合わせ、モデル比較や閾値調整に活かすヒントをまとめます。

Koefisien determinasi adalah nilai dalam statistik yang menyatakan seberapa besar variabel dependen (variabel tujuan) dijelaskan oleh variabel independen (variabel penjelas).

Umumnya, semakin tinggi semakin baik indikator penilaian
Kasus terbaik adalah 1.
Namun, semakin banyak fitur yang Anda tambahkan, skornya cenderung semakin tinggi.
Oleh karena itu, tidak mungkin untuk menilai “akurasi model yang tinggi” dengan melihat indikator ini saja

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
import numpy as np

import matplotlib.pyplot as plt

import japanize_matplotlib

from sklearn.datasets import make_regression

from sklearn.ensemble import RandomForestRegressor

from sklearn.model_selection import train_test_split

python

Membuat model dan menghitung koefisien determinasi untuk data sampel #

Pertama, mari kita buat data yang membuat prediksi lebih mungkin benar.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
X, y = make_regression(

    n_samples=1000,

    n_informative=3,

    n_features=20,

    random_state=RND,

)

train_X, test_X, train_y, test_y = train_test_split(

    X, y, test_size=0.33, random_state=RND

)

model = RandomForestRegressor(max_depth=5)

model.fit(train_X, train_y)

pred_y = model.predict(test_X)

python

Menghitung koefisien determinasi #

sklearn.metrics.roc_auc_score

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
from sklearn.metrics import r2_score

r2 = r2_score(test_y, pred_y)

y_min, y_max = np.min(test_y), np.max(test_y)

plt.figure(figsize=(6, 6))

plt.title(f"$R^2 =${r2}")

plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)

plt.scatter(test_y, pred_y, marker="x")

plt.xlabel("Jawaban yang benar")

plt.ylabel("Prediksi")

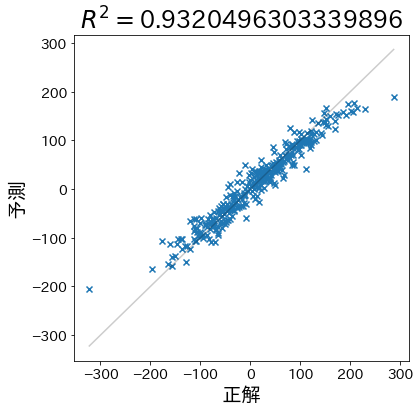
Menghitung koefisien determinasi (diagram)

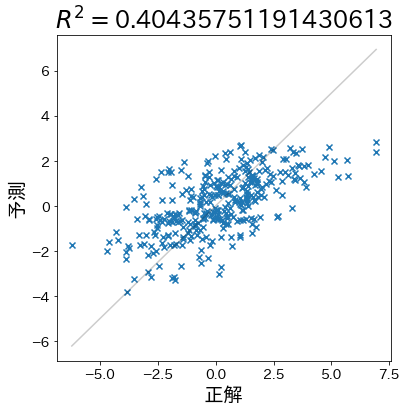
Selanjutnya, buatlah data yang prediksinya cenderung tidak benar dan periksa untuk melihat bahwa koefisien determinasi turun.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
X, y = make_regression(

    n_samples=1000,

    n_informative=3,

    n_features=20,

    effective_rank=4,

    noise=1.5,

    random_state=RND,

)

train_X, test_X, train_y, test_y = train_test_split(

    X, y, test_size=0.33, random_state=RND

)

model = RandomForestRegressor(max_depth=5)

model.fit(train_X, train_y)

pred_y = model.predict(test_X)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
r2 = r2_score(test_y, pred_y)

y_min, y_max = np.min(test_y), np.max(test_y)

plt.figure(figsize=(6, 6))

plt.title(f"$R^2 =${r2}")

plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)

plt.scatter(test_y, pred_y, marker="x")

plt.xlabel("Jawaban yang benar")

plt.ylabel("Prediksi")

Selanjutnya, buatlah data yang prediksinya cenderung tidak b… (diagram)

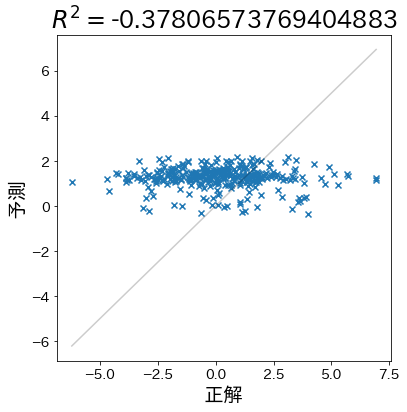
Ketika prediksi hampir acak #

Ketika akurasi bahkan lebih buruk daripada sekadar memprediksi rata-rata, koefisien determinasi adalah negatif.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
X, y = make_regression(

    n_samples=1000,

    n_informative=3,

    n_features=20,

    effective_rank=4,

    noise=1.5,

    random_state=RND,

)

train_X, test_X, train_y, test_y = train_test_split(

    X, y, test_size=0.33, random_state=RND

)

# Menyusun ulang train_y dan mengkonversi nilai secara acak

train_y = np.random.permutation(train_y)

train_y = np.sin(train_y) * 10 + 1

model = RandomForestRegressor(max_depth=1)

model.fit(train_X, train_y)

pred_y = model.predict(test_X)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
r2 = r2_score(test_y, pred_y)

y_min, y_max = np.min(test_y), np.max(test_y)

plt.figure(figsize=(6, 6))

plt.title(f"$R^2 =${r2}")

plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)

plt.scatter(test_y, pred_y, marker="x")

plt.xlabel("Jawaban yang benar")

plt.ylabel("Prediksi")

Ketika akurasi bahkan lebih buruk daripada sekadar mempredik… (diagram)

Koefisien determinasi ketika menggunakan metode kuadrat terkecil #

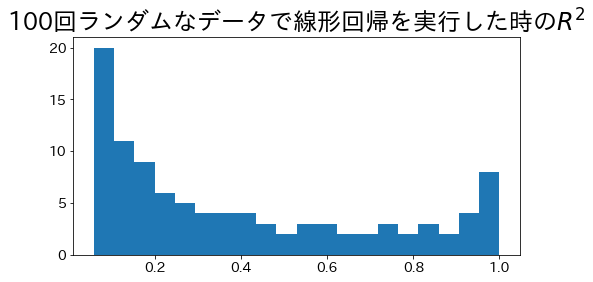
Dalam kasus garis regresi untuk regresi tunggal dengan menggunakan metode kuadrat terkecil, rentang koefisien determinasi adalah \( 0 \le R^2 \le 1\).

Mari kita coba mencari koefisien determinasi dengan menjalankan regresi 100 garis dengan noise acak pada data.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
from sklearn.linear_model import LinearRegression

from sklearn.pipeline import make_pipeline

from sklearn.preprocessing import StandardScaler

r2_scores = []

for i in range(100):

    X, y = make_regression(

        n_samples=500,

        n_informative=1,

        n_features=1,

        effective_rank=4,

        noise=i * 0.1,

        random_state=RND,

    )

    train_X, test_X, train_y, test_y = train_test_split(

        X, y, test_size=0.33, random_state=RND

    )

    # regresi linier

    model = make_pipeline(

        StandardScaler(with_mean=False), LinearRegression(positive=True)

    ).fit(train_X, train_y)

    # Menghitung koefisien determinasi

    pred_y = model.predict(test_X)

    r2 = r2_score(test_y, pred_y)

    r2_scores.append(r2)

plt.figure(figsize=(8, 4))

plt.hist(r2_scores, bins=20)

plt.show()

Mari kita coba mencari koefisien determinasi dengan menjalan… (diagram)