Memberi label anomali dengan statistik T^2 Hotelling

Diperbarui 2025-11-03 Baca 2 menit

<p><b>Statistik T^2 Hotelling</b> mengukur jarak Mahalanobis terhadap mean dan kovariansi. Pada data d-dimensi yang mendekati distribusi normal multivariat, \(T^2\) mengikuti distribusi \(\chi^2_d\) sehingga kita dapat menetapkan ambang berdasarkan tingkat signifikansi \(\alpha\).</p>

Rumus T^2 dan ambang (\chi^2) #

Untuk vektor fitur (x) dengan rata-rata (\mu) dan kovariansi (\Sigma):

$$ T^2 = (x - \mu)^\top \Sigma^{-1} (x - \mu) $$

Ambang deteksi anomali adalah

$$ \tau = \chi^2_d(1 - \alpha), $$

sehingga titik dengan (T^2 > \tau) dikategorikan sebagai anomali. Pada data satu dimensi, ini identik dengan kuadrat z-score.

Menyiapkan data contoh #

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
import numpy as np
import matplotlib.pyplot as plt

rng = np.random.default_rng(100)
n_samples = 500
time = np.arange(n_samples)
series = rng.normal(loc=0.0, scale=1.0, size=n_samples)

anomaly_index = rng.choice(n_samples, size=10, replace=False)
series[anomaly_index] += rng.normal(loc=6.0, scale=1.0, size=anomaly_index.size)

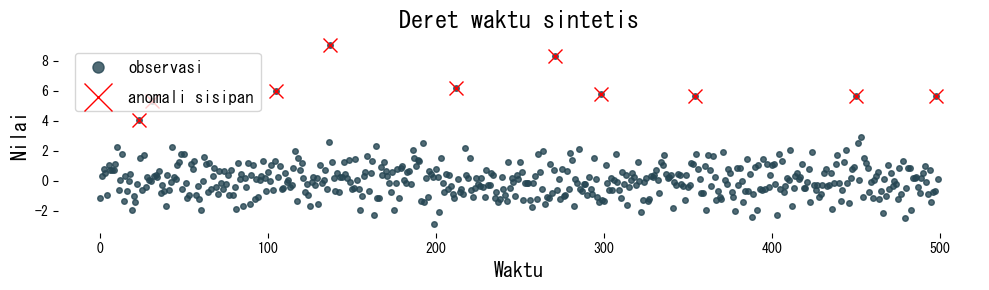
plt.figure(figsize=(10, 3))
plt.plot(time, series, ".", alpha=0.8, label="observasi")
plt.plot(anomaly_index, series[anomaly_index], "x", ms=10, c="red", label="anomali sisipan")
plt.title("Deret waktu sintetis")
plt.xlabel("Waktu")
plt.ylabel("Nilai")
plt.legend()
plt.tight_layout()
plt.show()

Menyiapkan data contoh (diagram)

Menghitung skor T^2 dan memberi label #

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from scipy.stats import chi2

def detect_hotelling_t2(series: np.ndarray, alpha: float = 0.05) -> tuple[np.ndarray, np.ndarray, float]:
    series = np.asarray(series)
    mean = series.mean()
    var = series.var(ddof=1)
    t2_scores = ((series - mean) ** 2) / var
    threshold = chi2.ppf(1 - alpha, df=1)
    detections = np.where(t2_scores > threshold)[0]
    return detections, t2_scores, threshold

detected_index, t2_scores, threshold = detect_hotelling_t2(series, alpha=0.05)

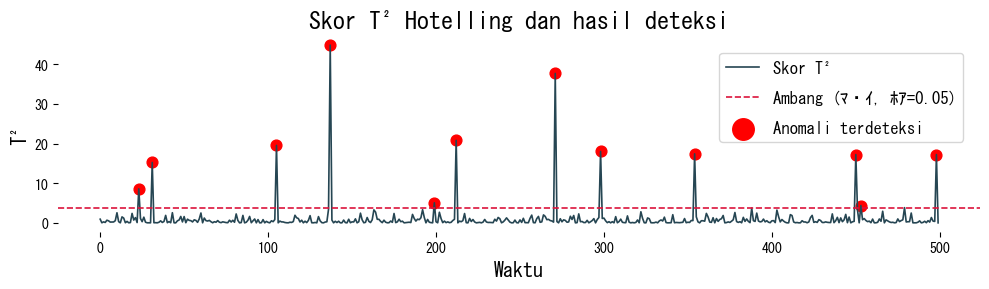
plt.figure(figsize=(10, 3))
plt.plot(time, t2_scores, label="Skor T^2")
plt.axhline(threshold, color="crimson", linestyle="--", label="Ambang (chi^2, alpha=0.05)")
plt.scatter(detected_index, t2_scores[detected_index], c="red", marker="o", s=60, label="Anomali terdeteksi")
plt.xlabel("Waktu")
plt.ylabel("T^2")
plt.title("Skor T^2 Hotelling dan hasil deteksi")
plt.legend()
plt.tight_layout()
plt.show()

Menghitung skor T^2 dan memberi label (diagram)

Catatan praktik #

Untuk dimensi tinggi, gunakan kovariansi penuh (\Sigma) dan pecahkan (\Sigma^{-1}(x - \mu)) sebagai sistem linear menggunakan scipy.linalg.solve (hindari menghitung invers secara eksplisit).
Pilih (\alpha) sesuai toleransi false positive. Dalam sistem pemantauan, nilai 0.01 atau lebih kecil sering dipakai untuk mengurangi alarm palsu.
Jika data jauh dari distribusi normal, kombinasikan dengan scaler yang robust (RobustScaler) atau transformasi daya sebelum menghitung T^2.
Pada pemantauan kontinu, perbarui estimasi mean dan kovariansi secara berkala agar model mengikuti drift.