Dynamic Time Warping (DTW)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import numpy as np

def dtw_distance(
    x: np.ndarray,
    y: np.ndarray,
    window: int | None = None,
) -> tuple[float, list[tuple[int, int]]]:
    n, m = len(x), len(y)
    window = max(window or max(n, m), abs(n - m))

    cost = np.full((n + 1, m + 1), np.inf)
    cost[0, 0] = 0.0

    for i in range(1, n + 1):
        for j in range(max(1, i - window), min(m + 1, i + window + 1)):
            dist = abs(x[i - 1] - y[j - 1])
            cost[i, j] = dist + min(cost[i - 1, j], cost[i, j - 1], cost[i - 1, j - 1])

    i, j = n, m
    path: list[tuple[int, int]] = []
    while i > 0 and j > 0:
        path.append((i - 1, j - 1))
        idx = np.argmin((cost[i - 1, j], cost[i, j - 1], cost[i - 1, j - 1]))
        if idx == 0:
            i -= 1
        elif idx == 1:
            j -= 1
        else:
            i -= 1
            j -= 1

    path.reverse()
    return cost[n, m], path

1
2

python --version  # contoh: Python 3.13.0
pip install matplotlib fastdtw

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

import matplotlib.pyplot as plt
from fastdtw import fastdtw

np.random.seed(42)
t = np.arange(0, 30)

series_a = 1.2 * np.sin(t / 2.0)
series_b = 1.1 * np.sin((t + 2) / 2.1) + 0.05 * np.random.randn(len(t))
series_c = 0.8 * np.cos(t / 2.0) + 0.05 * np.random.randn(len(t))

plt.figure(figsize=(10, 3))
plt.plot(t, series_a, label="Seri A", color="black")
plt.plot(t, series_b, label="Seri B", color="tab:red")
plt.plot(t, series_c, label="Seri C", color="tab:blue")
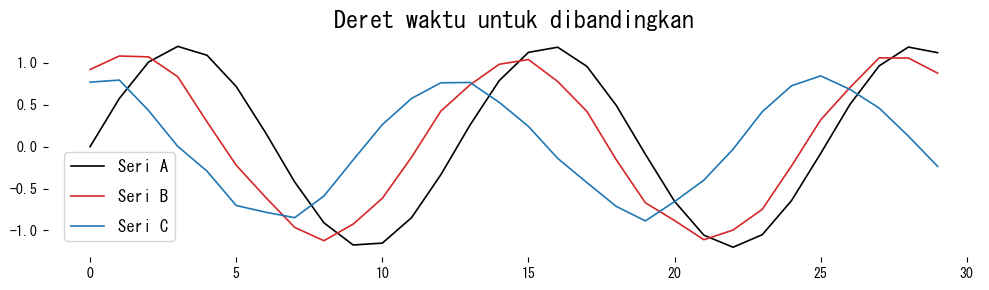
plt.title("Deret waktu untuk dibandingkan")
plt.legend()
plt.tight_layout()
plt.show()

1
2
3
4
5
6
7
8

dist_ab, path_ab = dtw_distance(series_a, series_b)
dist_ac, path_ac = dtw_distance(series_a, series_c)

fast_dist_ab, _ = fastdtw(series_a, series_b)
fast_dist_ac, _ = fastdtw(series_a, series_c)

print(f"DTW(A, B)  = {dist_ab:.3f}  / fastdtw = {fast_dist_ab:.3f}")
print(f"DTW(A, C)  = {dist_ac:.3f}  / fastdtw = {fast_dist_ac:.3f}")

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

def plot_warping(a: np.ndarray, b: np.ndarray, path: list[tuple[int, int]]) -> None:
    fig, axes = plt.subplots(
        1,
        2,
        figsize=(12, 4),
        gridspec_kw={"width_ratios": [1, 1.2]},
    )

    axes[0].plot(a, label="Seri A", color="black")
    axes[0].plot(b, label="Seri B", color="tab:red")
    axes[0].set_title("Deret waktu")
    axes[0].legend()

    axes[1].imshow(
        np.abs(np.subtract.outer(a, b)),
        origin="lower",
        interpolation="nearest",
        cmap="viridis",
    )
    path_arr = np.array(path)
    axes[1].plot(path_arr[:, 1], path_arr[:, 0], color="white", linewidth=2)
    axes[1].set_title("Biaya kumulatif dan jalur warping")
    axes[1].set_xlabel("Indeks Seri B")
    axes[1].set_ylabel("Indeks Seri A")
    plt.tight_layout()
    plt.show()

plot_warping(series_a, series_b, path_ab)