判別分析
線形判別分析(LDA)とは、二つのクラスのデータについて、クラスごとのデータのまとまり具合とクラス同士のデータのばらつき具合をもとに、クラスを判別できる境界線を引く手法です。また、求めた結果をもとにデータを次元削減することもできます。
このページではLDAで求めた決定境界を可視化して、次元削減した結果を可視化してみます。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.datasets import make_blobs
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
サンプル用データの作成
n_samples = 200
X, y = make_blobs(n_samples=200, centers=2, n_features=2, cluster_std=2)
X[:, 0] -= np.mean(X[:, 0])
X[:, 1] -= np.mean(X[:, 1])
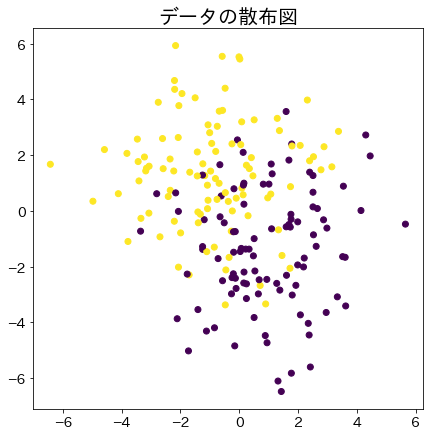
fig = plt.figure(figsize=(7, 7))
plt.title("データの散布図", fontsize=20)
plt.scatter(X[:, 0], X[:, 1], c=y)
plt.show()
線形判別分析法で決定境界を求める
# 決定境界を求める
clf = LinearDiscriminantAnalysis(store_covariance=True)
clf.fit(X, y)
# どのような決定境界が引かれたかを確認する
w = clf.coef_[0]
wt = -1 / (w[1] / w[0]) ## wに垂直な傾きを求める
xs = np.linspace(-10, 10, 100)
ys_w = [(w[1] / w[0]) * xi for xi in xs]
ys_wt = [wt * xi for xi in xs]
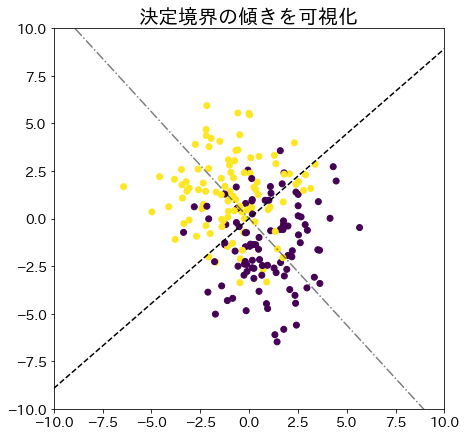
fig = plt.figure(figsize=(7, 7))
plt.title("決定境界の傾きを可視化", fontsize=20)
plt.scatter(X[:, 0], X[:, 1], c=y) # サンプルデータ
plt.plot(xs, ys_w, "-.", color="k", alpha=0.5) # wの向き
plt.plot(xs, ys_wt, "--", color="k") # wに垂直な向き
plt.xlim(-10, 10)
plt.ylim(-10, 10)
plt.show()
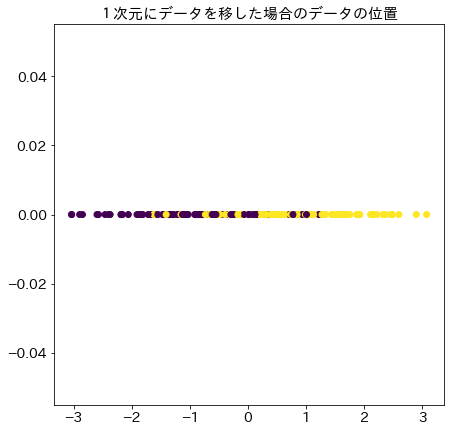
# 求めたベクトルwを元に1次元にデータを移した結果
X_1d = clf.transform(X).reshape(1, -1)[0]
fig = plt.figure(figsize=(7, 7))
plt.title("1次元にデータを移した場合のデータの位置", fontsize=15)
plt.scatter(X_1d, [0 for _ in range(n_samples)], c=y)
plt.show()
2次元以上のデータでの例
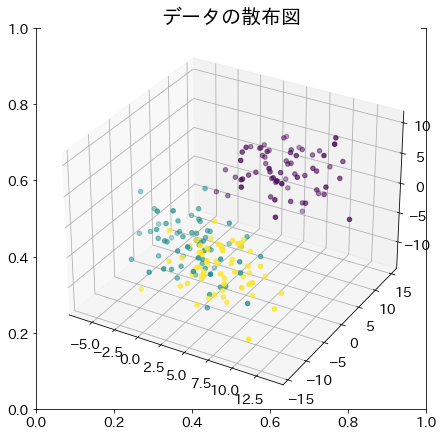
X_3d, y_3d = make_blobs(n_samples=200, centers=3, n_features=3, cluster_std=3)
# サンプルデータの分布
fig = plt.figure(figsize=(7, 7))
plt.title("データの散布図", fontsize=20)
ax = fig.add_subplot(projection="3d")
ax.scatter(X_3d[:, 0], X_3d[:, 1], X_3d[:, 2], c=y_3d)
plt.show()
# 線形判別分析を適用
clf_3d = LinearDiscriminantAnalysis()
clf_3d.fit(X_3d, y_3d)
X_2d = clf_3d.transform(X_3d)
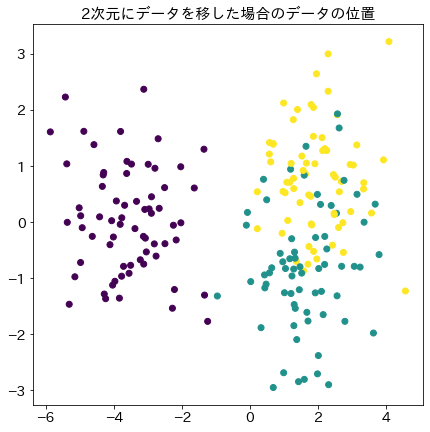
# 判別分析で次元削減した結果
fig = plt.figure(figsize=(7, 7))
plt.title("2次元にデータを移した場合のデータの位置", fontsize=15)
plt.scatter(X_2d[:, 0], X_2d[:, 1], c=y_3d)
plt.show()