ロジスティック回帰
ロジスティック回帰とは2クラス分類をするモデルです。線形回帰モデルが出力する数値を確率に変換するようにすることで、分類問題が解けるようにしています。
このページではsikit-learnに実装されているロジスティック回帰を実行し、その決定境界(分類の基準となる境界線)を引いてみます。
import matplotlib.pyplot as plt
import numpy as np
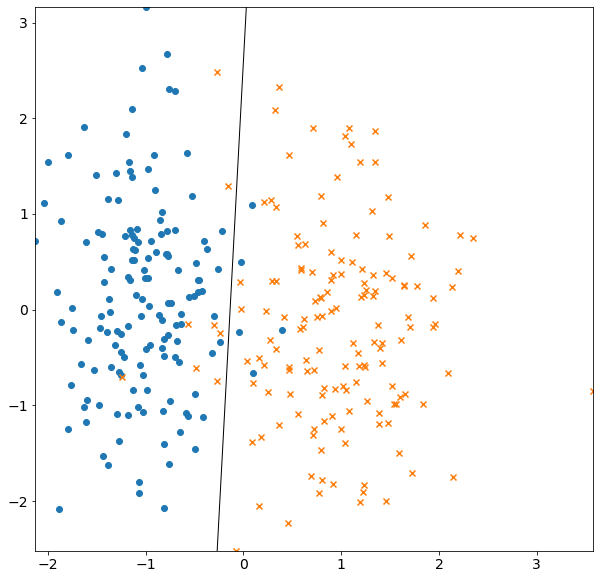
ロジット関数の可視化
fig = plt.figure(figsize=(4, 8))
p = np.linspace(0.01, 0.999, num=100)
y = np.log(p / (1 - p))
plt.plot(p, y)
plt.xlabel("p")
plt.ylabel("y")
plt.axhline(y=0, color="k")
plt.ylim(-3, 3)
plt.grid()
plt.show()
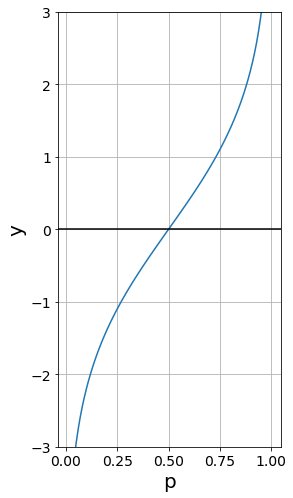
ロジスティック回帰
人工的に生成したデータに対してロジスティック回帰を実行します。
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
## データセット
X, Y = make_classification(
n_samples=300,
n_features=2,
n_redundant=0,
n_informative=1,
random_state=2,
n_clusters_per_class=1,
)
# ロジスティック回帰を学習
clf = LogisticRegression()
clf.fit(X, Y)
# 決定境界の直線を求める
b = clf.intercept_[0]
w1, w2 = clf.coef_.T
b_1 = -w1 / w2
b_0 = -b / w2
xmin, xmax = np.min(X[:, 0]), np.max(X[:, 0])
ymin, ymax = np.min(X[:, 1]), np.max(X[:, 1])
xd = np.array([xmin, xmax])
yd = b_1 * xd + b_0
# グラフを描画
plt.figure(figsize=(10, 10))
plt.plot(xd, yd, "k", lw=1, ls="-")
plt.scatter(*X[Y == 0].T, marker="o")
plt.scatter(*X[Y == 1].T, marker="x")
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.show()