PCA
PCA(主成分分析)とは教師なしアルゴリズムのひとつであり、次元削減をするアルゴリズムと見ることができます。多くの変数の情報を可能な限り損なわないように少数の変数に情報をまとめる手法と見ることができます。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.datasets import make_blobs
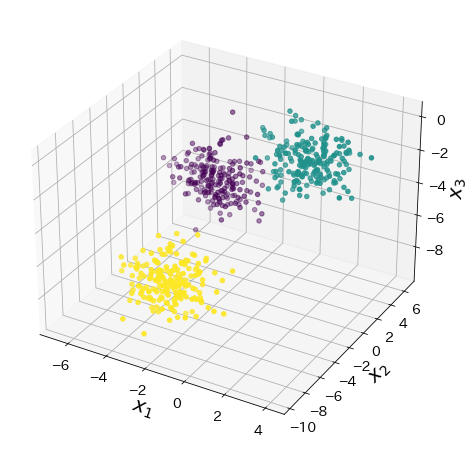
実験用のデータ
X, y = make_blobs(n_samples=600, n_features=3, random_state=117117)
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection="3d")
ax.scatter(X[:, 0], X[:, 1], X[:, 2], marker="o", c=y)
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.set_zlabel("$x_3$")
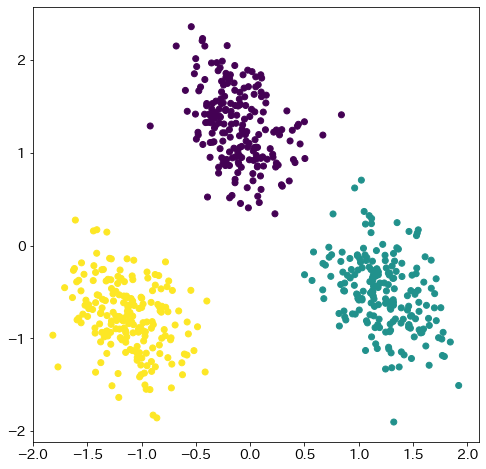
PCAで二次元に次元削減する
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
pca = PCA(n_components=2, whiten=True)
X_pca = pca.fit_transform(StandardScaler().fit_transform(X))
fig = plt.figure(figsize=(8, 8))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y)
正規化の効果を見る
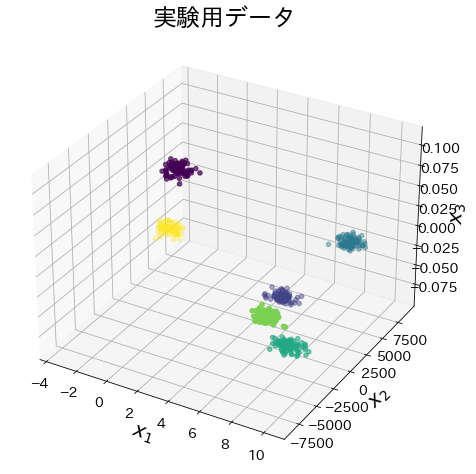
クラスタ数3, クラスタに重複がある場合
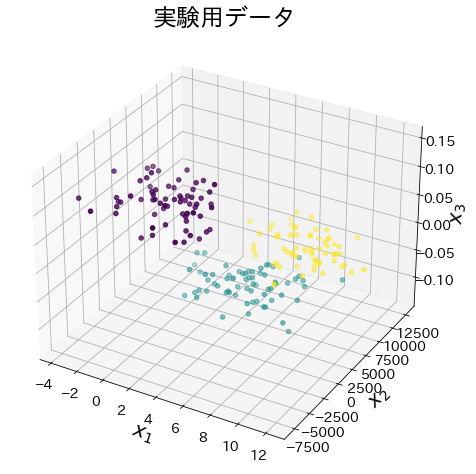
# 実験用データ
X, y = make_blobs(
n_samples=200, n_features=3, random_state=11711, centers=3, cluster_std=2.0
)
X[:, 1] = X[:, 1] * 1000
X[:, 2] = X[:, 2] * 0.01
X_ss = StandardScaler().fit_transform(X)
# 元データをプロット
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection="3d")
ax.scatter(X[:, 0], X[:, 1], X[:, 2], marker="o", c=y)
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.set_zlabel("$x_3$")
plt.title("実験用データ")
plt.show()
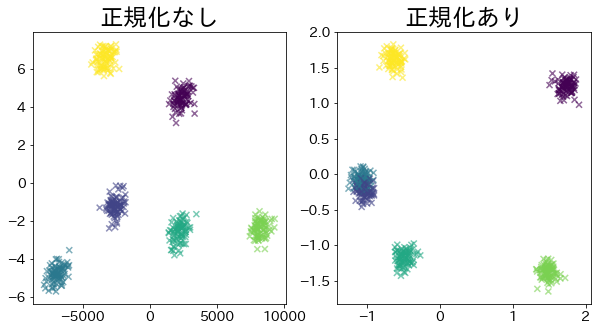
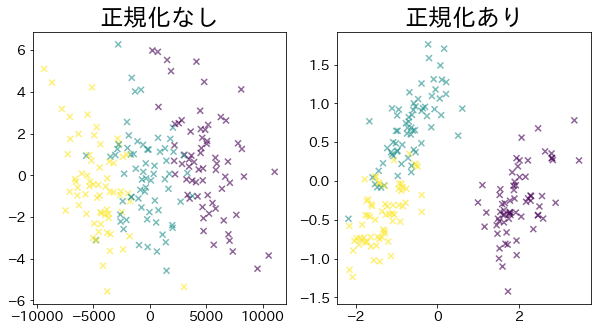
# 正規化をせずにPCA
pca = PCA(n_components=2).fit(X)
X_pca = pca.transform(X)
# 正規化をしてPCA
pca_ss = PCA(n_components=2).fit(X_ss)
X_pca_ss = pca_ss.transform(X_ss)
fig = plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.title("正規化なし")
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, marker="x", alpha=0.6)
plt.subplot(122)
plt.title("正規化あり")
plt.scatter(X_pca_ss[:, 0], X_pca_ss[:, 1], c=y, marker="x", alpha=0.6)
クラスタ数6, クラスタに重複が無い場合
# 実験用データ
X, y = make_blobs(
n_samples=500, n_features=3, random_state=11711, centers=6, cluster_std=0.4
)
X[:, 1] = X[:, 1] * 1000
X[:, 2] = X[:, 2] * 0.01
X_ss = StandardScaler().fit_transform(X)
# 元データをプロット
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection="3d")
ax.scatter(X[:, 0], X[:, 1], X[:, 2], marker="o", c=y)
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.set_zlabel("$x_3$")
plt.title("実験用データ")
plt.show()
# 正規化をせずにPCA
pca = PCA(n_components=2).fit(X)
X_pca = pca.transform(X)
# 正規化をしてPCA
pca_ss = PCA(n_components=2).fit(X_ss)
X_pca_ss = pca_ss.transform(X_ss)
fig = plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.title("正規化なし")
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, marker="x", alpha=0.6)
plt.subplot(122)
plt.title("正規化あり")
plt.scatter(X_pca_ss[:, 0], X_pca_ss[:, 1], c=y, marker="x", alpha=0.6)