勾配ブースティングの可視化
勾配ブースティングを用いた回帰について、仕組みを理解するために可視化をします。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.ensemble import GradientBoostingRegressor
訓練データに回帰モデルを当てはめる
# 訓練データ
n_samples = 500
X = np.linspace(-10, 10, n_samples)[:, np.newaxis]
noise = np.random.rand(X.shape[0]) * 10
# 目的変数
y = (np.sin(X).ravel()) * 10 + 10 + noise
# 回帰モデルを作成
n_estimators = 10
learning_rate = 0.5
reg = GradientBoostingRegressor(
n_estimators=n_estimators,
learning_rate=learning_rate,
)
reg.fit(X, y)
y_pred = reg.predict(X)
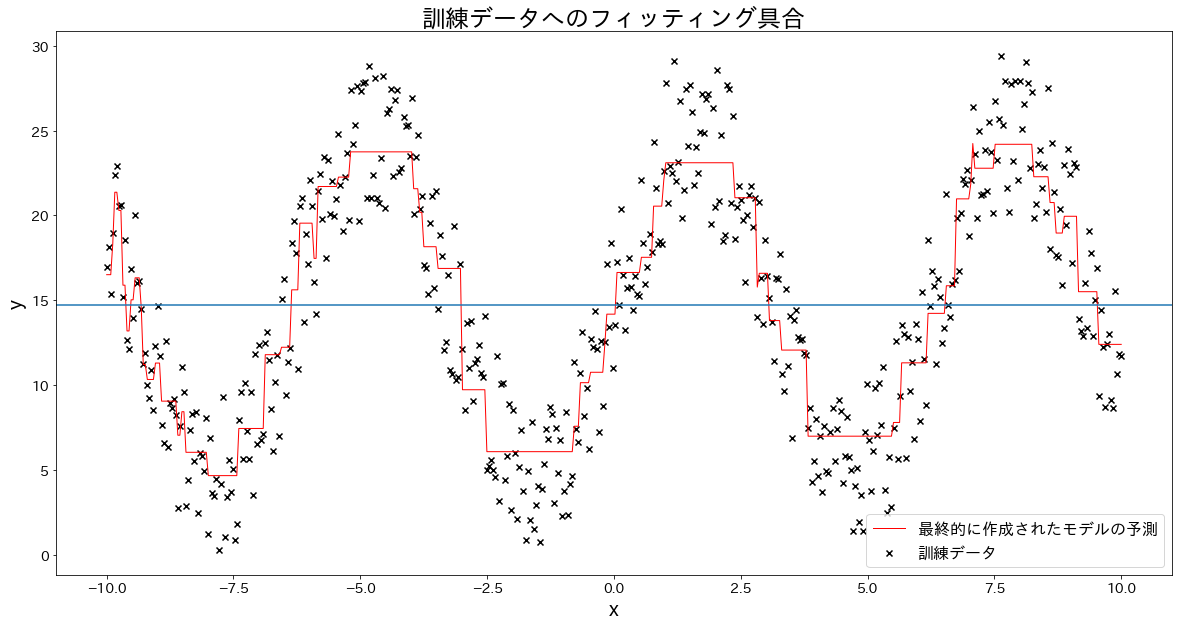
# 訓練データへのフィッティング具合を確認する
plt.figure(figsize=(20, 10))
plt.scatter(X, y, c="k", marker="x", label="訓練データ")
plt.plot(X, y_pred, c="r", label="最終的に作成されたモデルの予測", linewidth=1)
plt.xlabel("x")
plt.ylabel("y")
plt.axhline(y=np.mean(y))
plt.title("訓練データへのフィッティング具合")
plt.legend()
plt.show()
最終的な予測結果を木ごとに分解してみる
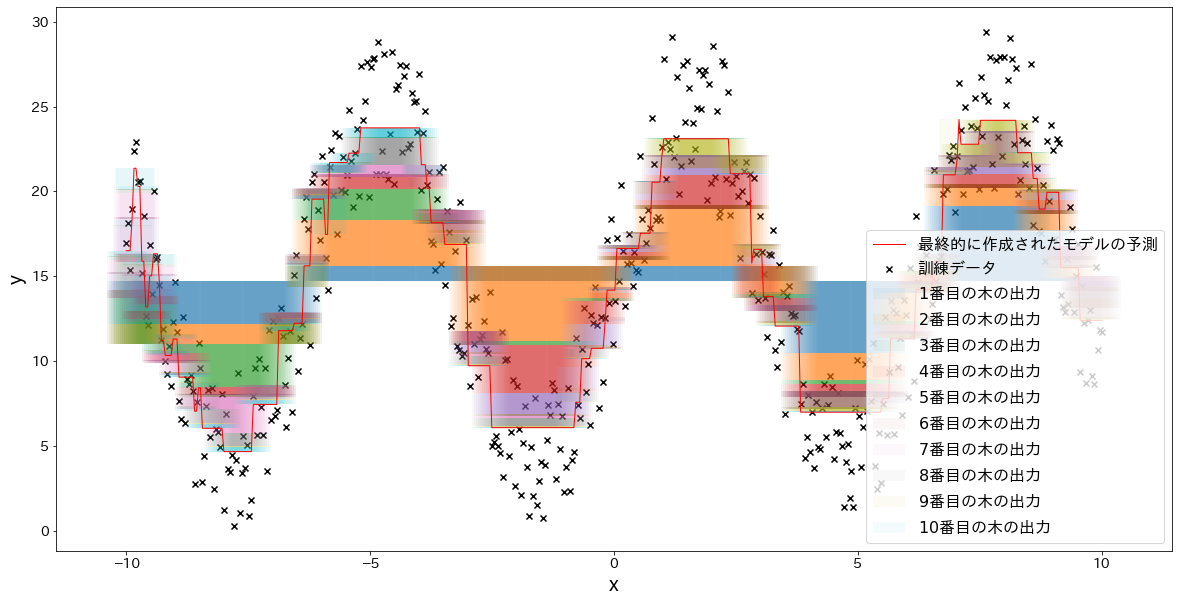
fig, ax = plt.subplots(figsize=(20, 10))
ind = np.arange(n_samples)
temp = np.zeros(n_samples) + np.mean(y)
for i in range(n_estimators):
res = reg.estimators_[i][0].predict(X) * learning_rate
ax.bar(X.flatten(), res, bottom=temp, label=f"${i+1}$番目の木の出力", alpha=0.05)
temp += res
plt.scatter(X.flatten(), y, c="k", marker="x", label="訓練データ")
plt.plot(X, y_pred, c="r", label="最終的に作成されたモデルの予測", linewidth=1)
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
Text(0, 0.5, 'y')
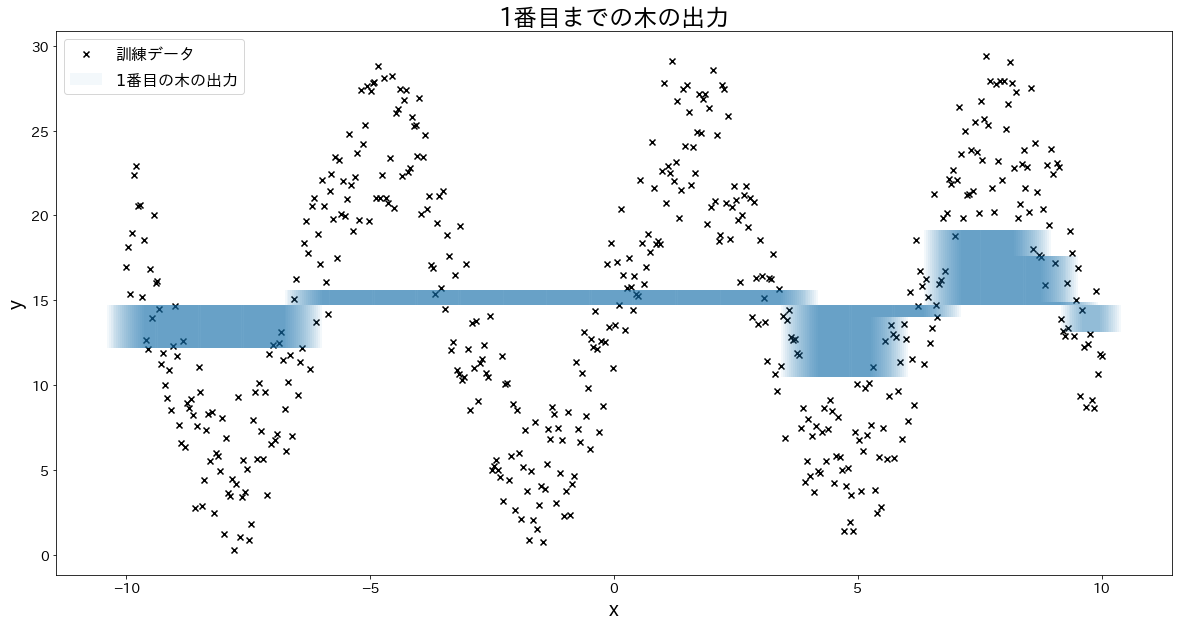
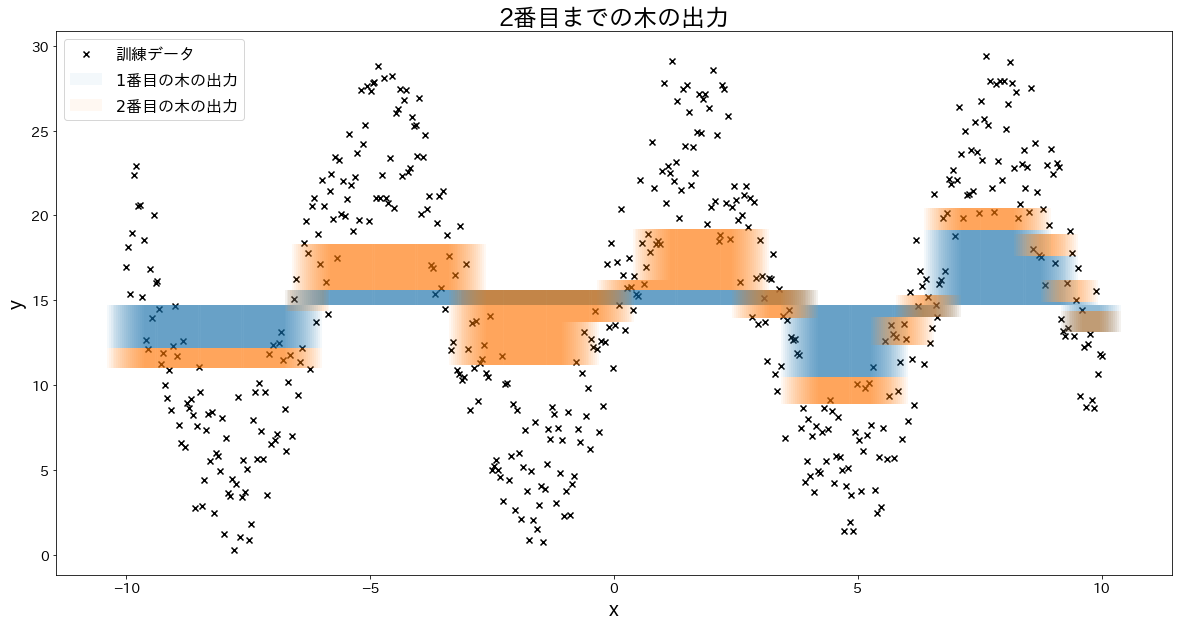
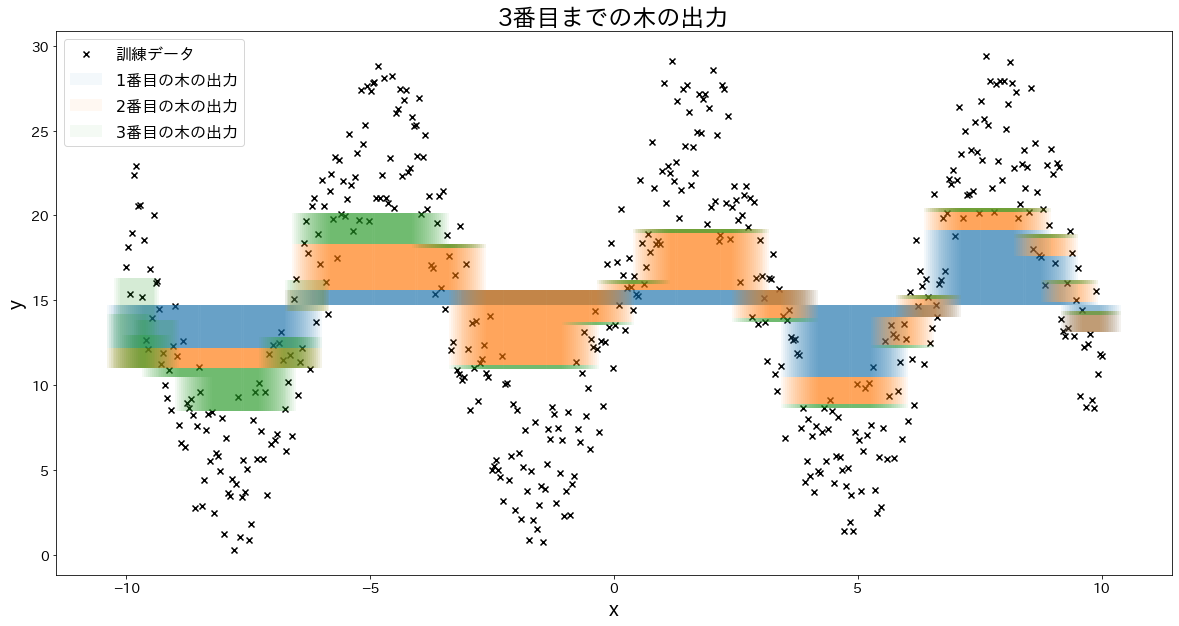
少しずつ誤差を修正していく様子を確認する
for i in range(5):
fig, ax = plt.subplots(figsize=(20, 10))
plt.title(f"{i+1}番目までの木の出力")
ind = np.arange(n_samples)
temp = np.zeros(n_samples) + np.mean(y)
for j in range(i + 1):
res = reg.estimators_[j][0].predict(X) * learning_rate
ax.bar(X.flatten(), res, bottom=temp, label=f"${j+1}$番目の木の出力", alpha=0.05)
temp += res
plt.scatter(X.flatten(), y, c="k", marker="x", label="訓練データ")
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
try:
plt.show()
except KeyboardInterrupt:
# TODO: jupyter bookのビルドで時間がかかるプロットが中断してしまうため、一時的に例外処理を挟む
break