外れ値と頑健性
外れ値とは他の値と比較して異常な値(非常に大きかったり、逆に小さかったりする値)の総称です。どのような値が外れ値であるかは、問題設定やデータの性質によって異なります。
このページでは、外れ値があるデータに対して「二乗誤差を用いて回帰をした」場合と「Huber損失を用いて回帰をした」場合の結果の違いを確認します。
import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
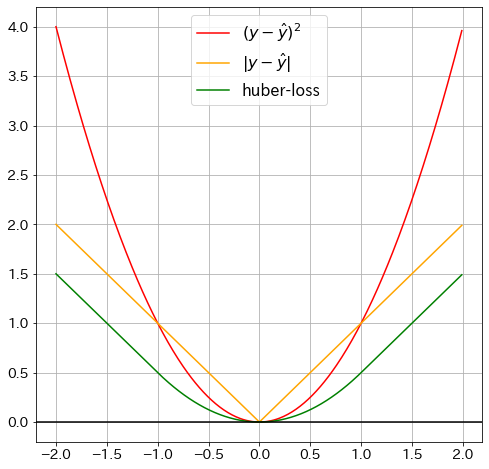
Huber損失の可視化
def huber_loss(y_pred: float, y: float, delta=1.0):
"""HuberLoss"""
huber_1 = 0.5 * (y - y_pred) ** 2
huber_2 = delta * (np.abs(y - y_pred) - 0.5 * delta)
return np.where(np.abs(y - y_pred) <= delta, huber_1, huber_2)
delta = 1.5
x_vals = np.arange(-2, 2, 0.01)
y_vals = np.where(
np.abs(x_vals) <= delta,
0.5 * np.square(x_vals),
delta * (np.abs(x_vals) - 0.5 * delta),
)
# グラフをプロットする
fig = plt.figure(figsize=(8, 8))
plt.plot(x_vals, x_vals ** 2, "red", label=r"$(y-\hat{y})^2$") ## 二乗誤差
plt.plot(x_vals, np.abs(x_vals), "orange", label=r"$|y-\hat{y}|$") ## 絶対誤差
plt.plot(
x_vals, huber_loss(x_vals * 2, x_vals), "green", label=r"huber-loss"
) # Huber-loss
plt.axhline(y=0, color="k")
plt.grid(True)
plt.legend()
plt.show()
最小二乗法との比較
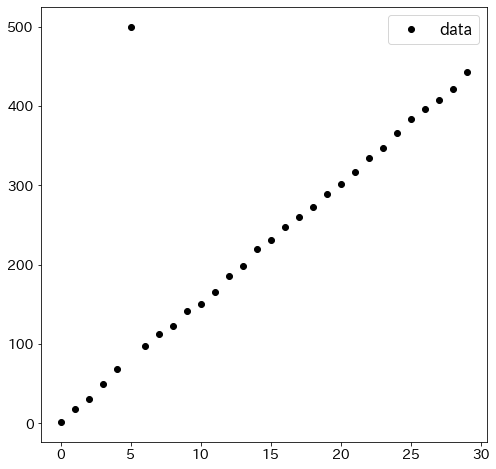
実験用のデータを作成する
Huber損失による回帰とが通常の線形回帰を比較するために、一つだけ外れ値を用意します。
N = 30
x1 = np.array([i for i in range(N)])
x2 = np.array([i for i in range(N)])
X = np.array([x1, x2]).T
epsilon = np.array([np.random.random() for i in range(N)])
y = 5 * x1 + 10 * x2 + epsilon * 10
y[5] = 500
plt.figure(figsize=(8, 8))
plt.plot(x1, y, "ko", label="data")
plt.legend()
plt.show()
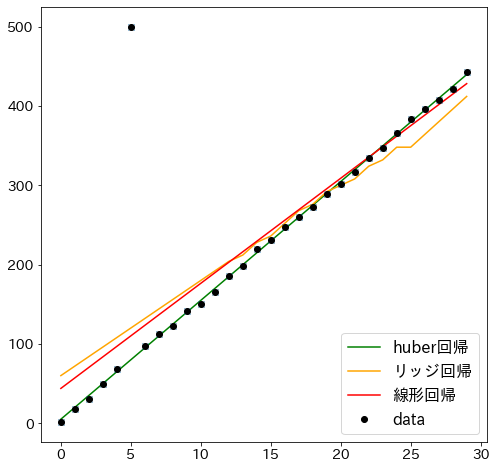
最小二乗法とリッジ回帰を当てはめた場合と比較する
from sklearn.datasets import make_regression
from sklearn.linear_model import HuberRegressor, Ridge
from sklearn.linear_model import LinearRegression
plt.figure(figsize=(8, 8))
huber = HuberRegressor(alpha=0.0, epsilon=3)
huber.fit(X, y)
plt.plot(x1, huber.predict(X), "green", label="huber回帰")
ridge = Ridge(alpha=0.0, random_state=0)
ridge.fit(X, y)
plt.plot(x1, ridge.predict(X), "orange", label="リッジ回帰")
lr = LinearRegression()
lr.fit(X, y)
plt.plot(x1, lr.predict(X), "r-", label="線形回帰")
plt.plot(x1, y, "x")
plt.plot(x1, y, "ko", label="data")
plt.legend()
plt.show()