決定係数
決定係数(けっていけいすう、(英: coefficient of determination、R2)は、統計学において、独立変数(説明変数)が従属変数(目的変数)のどれくらいを説明できるかを表す値である。寄与率と呼ばれることもある。 出典: 決定係数 出典: フリー百科事典『ウィキペディア(Wikipedia)』
- 一般に高ければ高いほどよい評価指標
- 最も良い場合に1になる
- ただし、特徴を増やせば増やすほど高くなる傾向にある
- この指標だけを見て「モデルの精度が高い」とは判断できない
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.datasets import make_regression
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
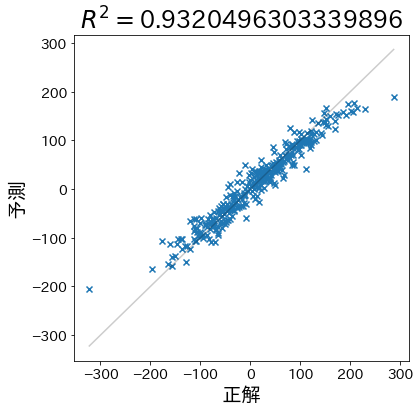
サンプルデータに対してモデルを作成し決定係数を計算
予測が当たりやすいデータを作成
X, y = make_regression(
n_samples=1000,
n_informative=3,
n_features=20,
random_state=RND,
)
train_X, test_X, train_y, test_y = train_test_split(
X, y, test_size=0.33, random_state=RND
)
model = RandomForestRegressor(max_depth=5)
model.fit(train_X, train_y)
pred_y = model.predict(test_X)
決定係数を計算
from sklearn.metrics import r2_score
r2 = r2_score(test_y, pred_y)
y_min, y_max = np.min(test_y), np.max(test_y)
plt.figure(figsize=(6, 6))
plt.title(f"$R^2 =${r2}")
plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)
plt.scatter(test_y, pred_y, marker="x")
plt.xlabel("正解")
plt.ylabel("予測")
Text(0, 0.5, '予測')
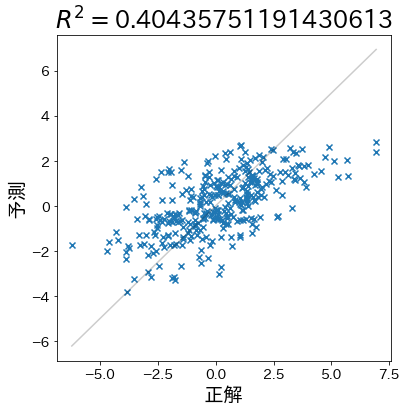
予測が当たりにくいデータを作成
決定係数が下がることを確認します。
X, y = make_regression(
n_samples=1000,
n_informative=3,
n_features=20,
effective_rank=4,
noise=1.5,
random_state=RND,
)
train_X, test_X, train_y, test_y = train_test_split(
X, y, test_size=0.33, random_state=RND
)
model = RandomForestRegressor(max_depth=5)
model.fit(train_X, train_y)
pred_y = model.predict(test_X)
r2 = r2_score(test_y, pred_y)
y_min, y_max = np.min(test_y), np.max(test_y)
plt.figure(figsize=(6, 6))
plt.title(f"$R^2 =${r2}")
plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)
plt.scatter(test_y, pred_y, marker="x")
plt.xlabel("正解")
plt.ylabel("予測")
Text(0, 0.5, '予測')
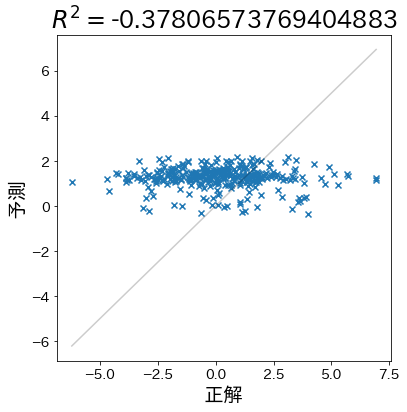
予測がデタラメな場合
単純に平均を予測するよりも更に精度が悪い時、決定係数がマイナスになることを確認します。
X, y = make_regression(
n_samples=1000,
n_informative=3,
n_features=20,
effective_rank=4,
noise=1.5,
random_state=RND,
)
train_X, test_X, train_y, test_y = train_test_split(
X, y, test_size=0.33, random_state=RND
)
# train_yをランダムに並び替え、さらに値を変換する
train_y = np.random.permutation(train_y)
train_y = np.sin(train_y) * 10 + 1
model = RandomForestRegressor(max_depth=1)
model.fit(train_X, train_y)
pred_y = model.predict(test_X)
r2 = r2_score(test_y, pred_y)
y_min, y_max = np.min(test_y), np.max(test_y)
plt.figure(figsize=(6, 6))
plt.title(f"$R^2 =${r2}")
plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)
plt.scatter(test_y, pred_y, marker="x")
plt.xlabel("正解")
plt.ylabel("予測")
Text(0, 0.5, '予測')
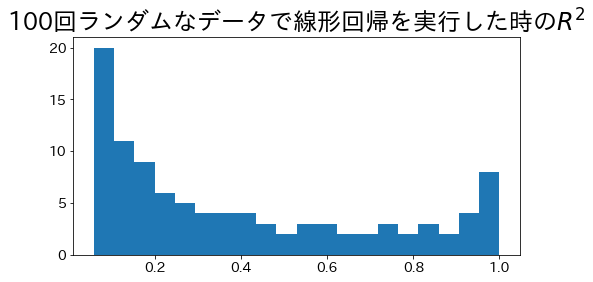
最小二乗法を使用した時の決定係数
最小二乗法による単回帰の回帰直線の場合、決定係数の範囲が $ 0 \le R^2 \le 1$ になります。 データにランダムにノイズを載せて、100回線形回帰を実行し決定係数を求めてみます。
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
r2_scores = []
for i in range(100):
# データ作成
X, y = make_regression(
n_samples=500,
n_informative=1,
n_features=1,
effective_rank=4,
noise=i * 0.1,
random_state=RND,
)
train_X, test_X, train_y, test_y = train_test_split(
X, y, test_size=0.33, random_state=RND
)
# 線形回帰
model = make_pipeline(
StandardScaler(with_mean=False), LinearRegression(positive=True)
).fit(train_X, train_y)
# 決定係数を算出
pred_y = model.predict(test_X)
r2 = r2_score(test_y, pred_y)
r2_scores.append(r2)
plt.figure(figsize=(8, 4))
plt.title("100回ランダムなデータで線形回帰を実行した時の$R^2$")
plt.hist(r2_scores, bins=20)
plt.show()