投資信託
投資信託で効率的フロンティアを計算してみる
2014091602: AB・米国成長株投信Dコース(H無) 予想分配金2018103105:eMAXIS Slim全世界株式(オール・カントリー)2015042708: ニッセイ TOPIXインデックスファンド2019092601: SBI・V・S&P500インデックス・ファンド2018070301: eMAXIS Slim米国株式(S&P500)2011020701: 三菱UFJ 純金ファンド(←保有していないですが金価格の参考として)
データの読み込み
WEALTH ADVISERから手動で取得した週次のcsvデータを使用して、効率的フロンティアを計算してみます。
import os
import pandas as pd
データ保存先ディレクトリ = "C://Users//nanja-win-ms//Dropbox//PC//Downloads//"
投資信託一覧 = {
"2018103105": "eMAXIS Slim全世界株式(オール・カントリー)",
"2015042708": "ニッセイ TOPIXインデックスファンド",
"2019092601": "SBI・V・S&P500インデックス・ファンド",
"2018070301": "eMAXIS Slim米国株式(S&P500)",
"2011020701": "三菱UFJ 純金ファンド",
}
投資信託リターン = {}
for 投資信託ID, 投資信託名 in 投資信託一覧.items():
月次リターンファイル名 = [
c
for c in os.listdir(os.path.join(データ保存先ディレクトリ, 投資信託ID))
if c.startswith("基準価額")
][0]
投資信託リターン[投資信託ID] = pd.read_csv(
os.path.join(データ保存先ディレクトリ, 投資信託ID, 月次リターンファイル名), encoding="cp932"
)
投資信託リターン[投資信託ID].columns = ["日付", 投資信託名]
データの整形
x=日付、y=銘柄名のデータを作成します。投資信託でなく株式でも可能です。
ポートフォリオ = None
for 投資信託ID in 投資信託一覧.keys():
if ポートフォリオ is None:
ポートフォリオ = 投資信託リターン[投資信託ID]
else:
ポートフォリオ = pd.merge(ポートフォリオ, 投資信託リターン[投資信託ID], on="日付")
ポートフォリオ.index = pd.to_datetime(ポートフォリオ["日付"], format="%Y%m%d")
ポートフォリオ.drop("日付", axis=1, inplace=True)
ポートフォリオ
| eMAXIS Slim全世界株式(オール・カントリー) | ニッセイ TOPIXインデックスファンド | SBI・V・S&P500インデックス・ファンド | eMAXIS Slim米国株式(S&P500) | 三菱UFJ 純金ファンド | |
|---|---|---|---|---|---|
| 日付 | |||||
| 2020-01-10 | 11828 | 11720 | 11203 | 12185 | 13827 |
| 2020-01-17 | 12036 | 11723 | 11429 | 12428 | 14063 |
| 2020-01-24 | 11932 | 11689 | 11381 | 12378 | 14008 |
| 2020-01-31 | 11667 | 11379 | 11189 | 12168 | 14085 |
| 2020-02-07 | 11987 | 11703 | 11490 | 12496 | 14242 |
| ... | ... | ... | ... | ... | ... |
| 2023-12-29 | 20899 | 17484 | 22229 | 24281 | 23054 |
| 2024-01-05 | 20972 | 17684 | 22285 | 24342 | 23270 |
| 2024-01-12 | 21283 | 18428 | 22763 | 24871 | 23226 |
| 2024-01-19 | 21536 | 18543 | 23219 | 25369 | 23562 |
| 2024-01-26 | 21916 | 18450 | 23699 | 25888 | 23437 |
212 rows × 5 columns
可視化
import japanize_matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
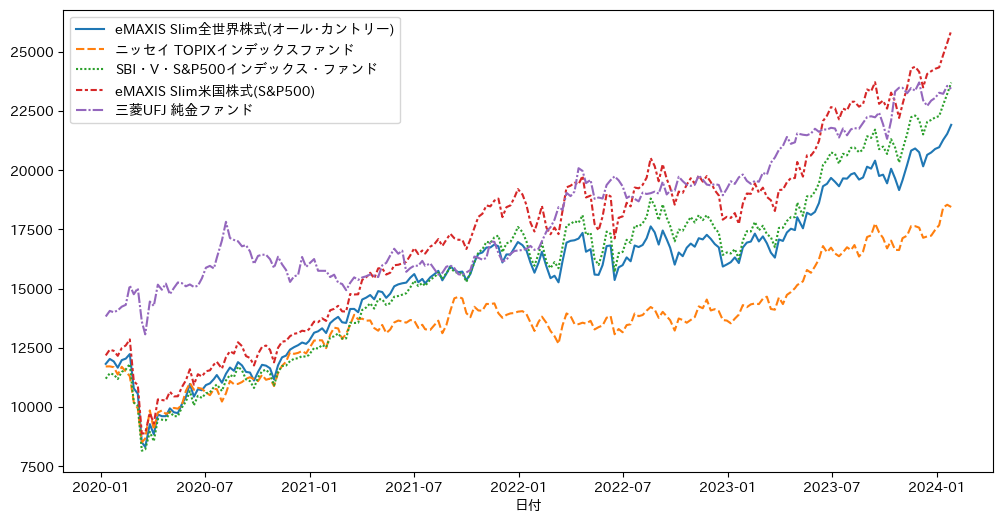
plt.figure(figsize=(12, 6))
sns.lineplot(data=ポートフォリオ)
<Axes: xlabel='日付'>
from pypfopt import expected_returns, risk_models
from pypfopt.efficient_frontier import EfficientFrontier
mu = expected_returns.mean_historical_return(ポートフォリオ)
S = risk_models.sample_cov(ポートフォリオ)
ef = EfficientFrontier(mu, S)
weights = ef.max_sharpe()
ef.portfolio_performance(verbose=True)
Expected annual return: 115.5%
Annual volatility: 34.2%
Sharpe Ratio: 3.32
(1.1546507705298557, 0.34188826020611157, 3.318776637272708)
from pypfopt import CLA, plotting
cla = CLA(mu, S)
cla.max_sharpe()
cla.portfolio_performance(verbose=True)
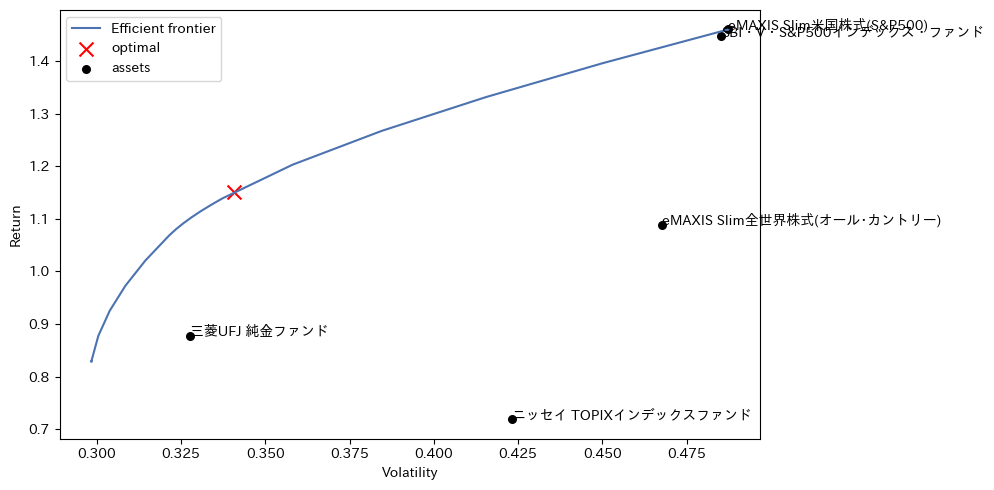
plt.figure(figsize=(10, 5))
plotting.plot_efficient_frontier(cla, show_assets=True, points=50, show_tickers=True)
Expected annual return: 115.1%
Annual volatility: 34.1%
Sharpe Ratio: 3.32
<Axes: xlabel='Volatility', ylabel='Return'>
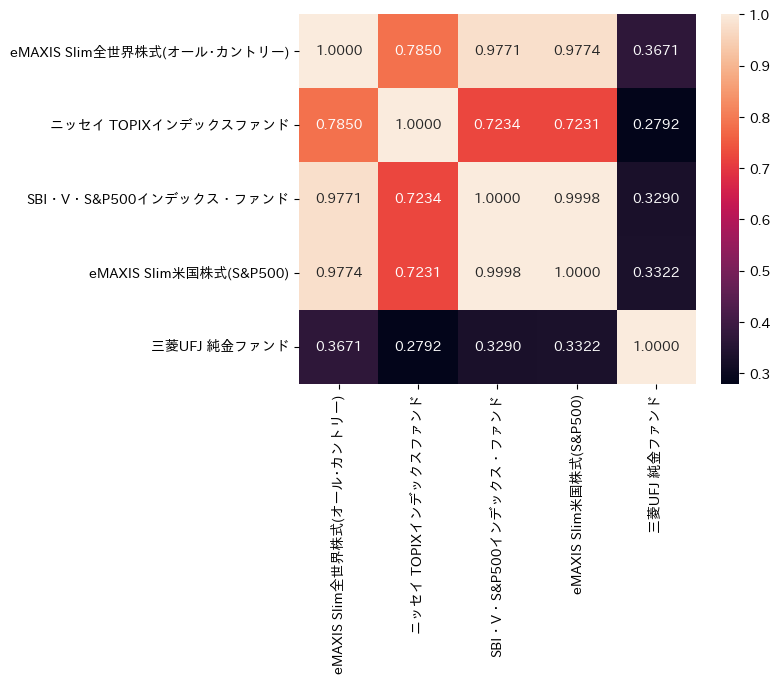
値動きの相関
値動きの変化で相関を計算してみます。
sns.heatmap(ポートフォリオ.diff().dropna().corr(), annot=True, fmt="1.4f")
<Axes: >