Box-Cox変換
モデルを使って時系列データを分析するためには前処理が必要な場合があります。時系列モデルはどんなデータでも分析可能というわけではなく、「分散が常に一定」「正規分布に従っている」などの仮定をおいていることが多いからです。
ここではBox-Cox変換を用いて、少し偏りのあるデータを正規分布に近い形に変換し、それがモデルの出力(正解と予測値の誤差の分布)にどのような影響があるかを見てみます。
import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import numpy as np
plt.figure(figsize=(12, 5))
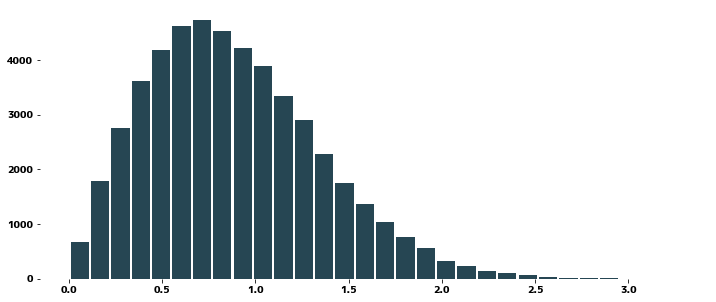
data_wb = np.random.weibull(2.0, size=50000)
plt.hist(data_wb, bins=30, rwidth=0.9)
plt.show()
plt.figure(figsize=(12, 5))
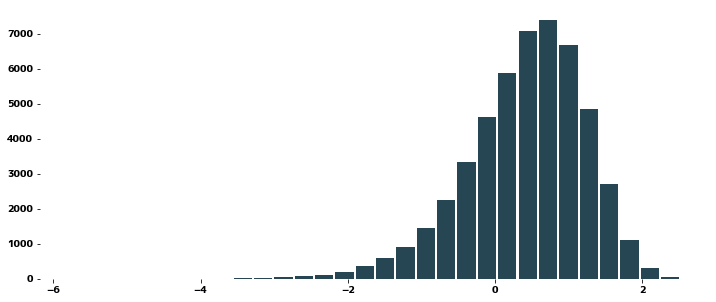
data_lg = stats.loggamma.rvs(2.0, size=50000)
plt.hist(data_lg, bins=30, rwidth=0.9)
plt.show()
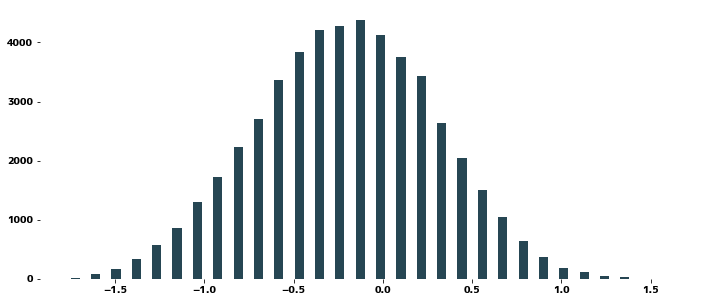
from scipy.stats import boxcox
plt.figure(figsize=(12, 5))
plt.hist(boxcox(data_wb), bins=30, rwidth=0.9)
plt.show()
try:
plt.figure(figsize=(12, 5))
plt.hist(boxcox(data_lg), bins=30, rwidth=0.9)
plt.show()
except ValueError as e:
print(f"エラーの内容: ValueError {e.args}")
エラーの内容: ValueError ('Data must be positive.',)
<Figure size 864x360 with 0 Axes>
from scipy.stats import yeojohnson
plt.figure(figsize=(12, 5))
plt.hist(yeojohnson(data_lg), bins=30, rwidth=0.9)
plt.show()
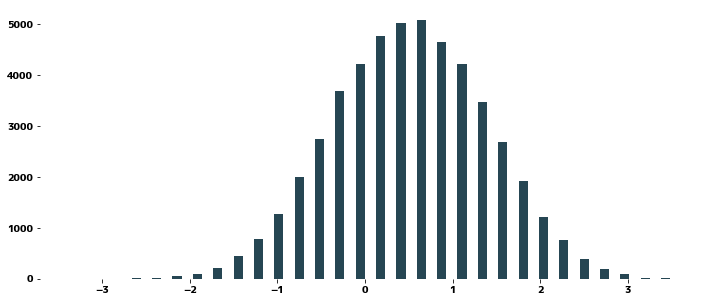
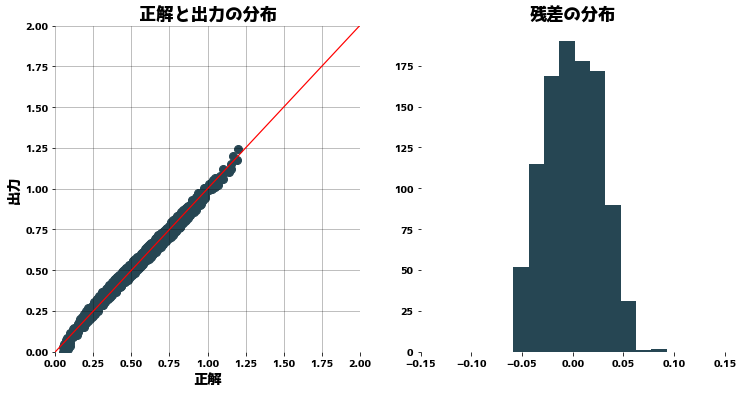
リッジ回帰をフィッティングしてみる
yの分布を正規分布に近づけずにリッジ回帰を適用した場合は、残差の分布に偏りがあることがわかります。
from sklearn.linear_model import Ridge
N = 1000
rng = np.random.RandomState(0)
y = np.random.weibull(2.0, size=N)
X = rng.randn(N, 5)
X[:, 0] = np.sqrt(y) + np.random.rand(N) / 10
plt.figure(figsize=(12, 5))
plt.hist(y, bins=20, rwidth=0.9)
plt.title("yの分布")
plt.show()
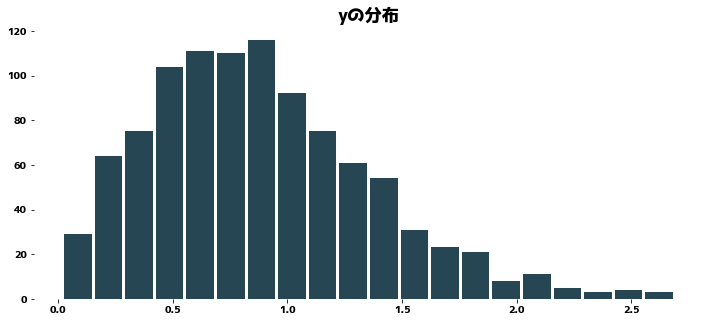
clf = Ridge(alpha=1.0)
clf.fit(X, y)
pred = clf.predict(X)
plt.figure(figsize=(12, 6))
plt.subplot(121)
plt.title("正解と出力の分布")
plt.scatter(y, pred)
plt.plot([0, 2], [0, 2], "r")
plt.xlabel("正解")
plt.ylabel("出力")
plt.xlim(0, 2)
plt.ylim(0, 2)
plt.grid()
plt.subplot(122)
plt.title("残差の分布")
plt.hist(y - pred)
plt.xlim(-0.5, 0.5)
plt.show()
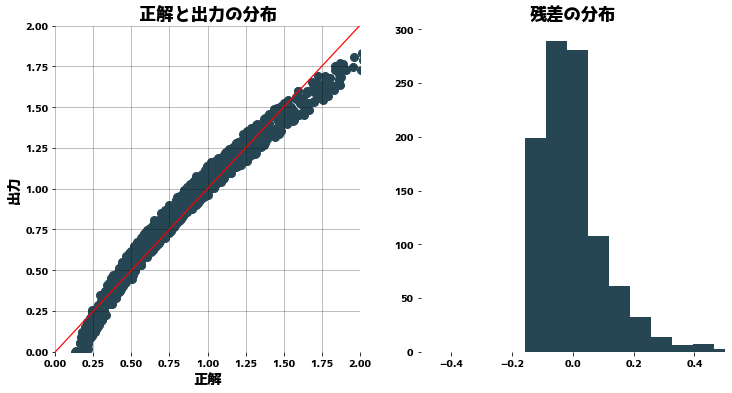
clf = Ridge(alpha=1.0)
clf.fit(X, yeojohnson(y)[0])
pred = clf.predict(X)
plt.figure(figsize=(12, 6))
plt.subplot(121)
plt.title("正解と出力の分布")
plt.scatter(yeojohnson(y)[0], pred)
plt.plot([0, 2], [0, 2], "r")
plt.xlabel("正解")
plt.ylabel("出力")
plt.xlim(0, 2)
plt.ylim(0, 2)
plt.grid()
plt.subplot(122)
plt.title("残差の分布")
plt.hist(yeojohnson(y)[0] - pred)
plt.xlim(-0.15, 0.15)
plt.show()