DDTW(Derivative-DTW)
Keogh, Eamonn J., and Michael J. Pazzani. “Derivative dynamic time warping.” Proceedings of the 2001 SIAM international conference on data mining. Society for Industrial and Applied Mathematics, 2001. (pdf) の式を参考に実装しています
DDTW(Derivative-DTW)はDTWから派生した手法であり、時系列の変化具合に着目した手法。数値の誤差そのものではなく、変化量の違いに着目して類似度を測ります。
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import japanize_matplotlib
from IPython.display import display, HTML
from utils import get_finance_data
import warnings
warnings.filterwarnings("ignore") # TODO: フォントが見つからない場合のwarning抑制
Derivative DTW
pythonで実行できるライブラリがすぐに見つけられなかったので、実装してみました。
def DDTW(Q, C):
"""
Args:
Q (np.array or list): 一つ目の波形
C (np.array or list): 二つ目の波形
Returns:
γ_mat (np.array): DDTWを計算するための行列
arrows (np.array): 各時点で←・↙︎・↓のどのマスが最小だったかを示す記号を保存する行列
ddtw (float): DDTW
"""
Q, C = np.array(Q), np.array(C)
assert Q.shape[0] > 3, "一つ目の波形のフォーマットがおかしいです。"
assert C.shape[0] > 3, "二つ目の波形のフォーマットがおかしいです。"
# 3.1 Algorithm details の式
def _Dq(q):
return ((q[1] - q[0]) + (q[2] - q[0]) / 2) / 2
# 二つの時点間の距離
def _γ(x, y):
return abs(_Dq(x) - _Dq(y))
# 各変数
n, m = Q.shape[0] - 2, C.shape[0] - 2
γ_mat = np.zeros((n, m))
arrows = np.array(np.zeros((n, m)), dtype=str) # 可視化用の行列でDDTWの値とは無関係
# 一番左下のスタート地点
γ_mat[0, 0] = _γ(Q[0:3], C[0:3])
# 一列目を計算
for i in range(1, n):
γ_mat[i, 0] = γ_mat[i - 1, 0] + _γ(Q[i - 1 : i + 2], C[0:3])
arrows[i, 0] = "↓"
# 一行目を計算
for j in range(1, m):
γ_mat[0, j] = γ_mat[0, j - 1] + _γ(Q[0:3], C[j - 1 : j + 2])
arrows[0, j] = "←"
# 残りのマスを計算
for i in range(1, n):
for j in range(1, m):
# DDTWを求めるためのマトリクスを埋める
d_ij = _γ(Q[i - 1 : i + 2], C[j - 1 : j + 2])
γ_mat[i, j] = d_ij + np.min(
[γ_mat[i - 1, j - 1], γ_mat[i - 1, j], γ_mat[i, j - 1]]
)
# 矢印を書くための行列(DDTWの値とは関係無い処理)
if (
square_index := np.argmin(
[γ_mat[i - 1, j - 1], γ_mat[i - 1, j], γ_mat[i, j - 1]]
)
) == 0:
arrows[i, j] = "↙︎"
elif square_index == 1:
arrows[i, j] = "↓"
elif square_index == 2:
arrows[i, j] = "←"
return γ_mat, arrows, γ_mat[n - 1, m - 1]
サンプルデータを確認する
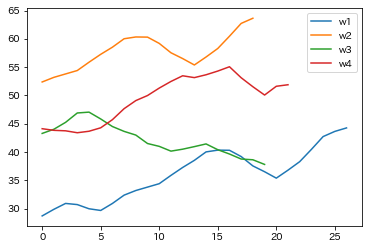
実験に使用するデータを確認します。波形の長さはそれぞれ異なり、平均値もバラバラです。
- $w_1$と$w_2$は形が近いが、平均値が乖離している
- $w_2$と$w_4$は平均値が近いが、形が違う
# 銘柄名、期間、保存先ファイル
ticker_symbol = "ZIM"
start = "2021-01-01"
end = "2022-01-01"
# データを取得する
df1 = get_finance_data(ticker_symbol, start=start, end=end, savedir="data")
df1["Close"] = df1["Close"].rolling(window=3).mean().fillna(0)
w1, w2 = df1["Close"][53:80].values, df1["Close"][60:79].values + 20
w3, w4 = df1["Close"][100:120].values, df1["Close"][145:167].values - 5
plt.plot(w1, label="w1")
plt.plot(w2, label="w2")
plt.plot(w3, label="w3")
plt.plot(w4, label="w4")
plt.legend()
<matplotlib.legend.Legend at 0x7f8cb27e7dc0>
同じ波形を比較
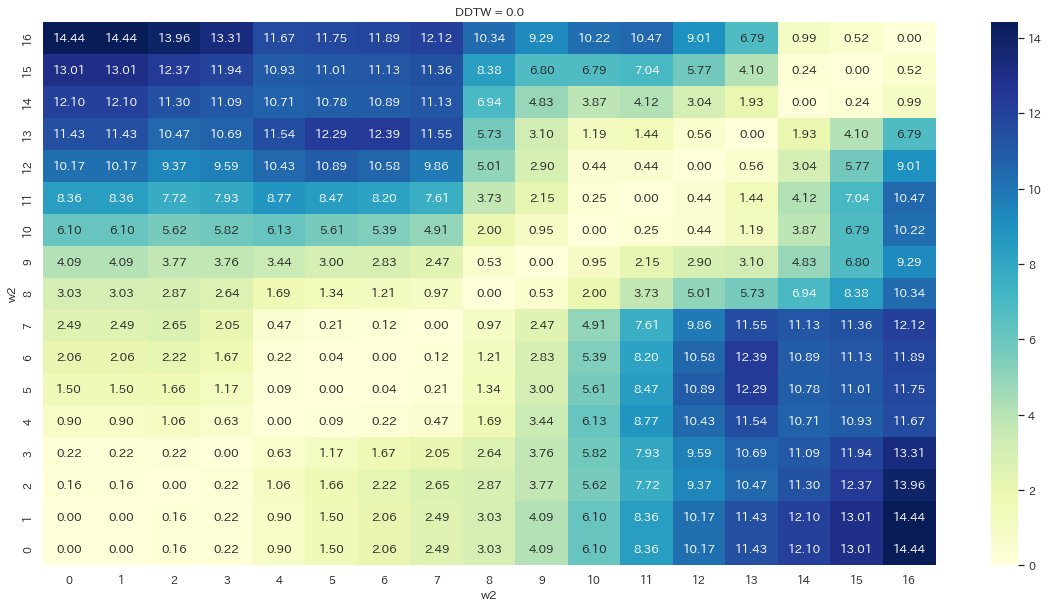
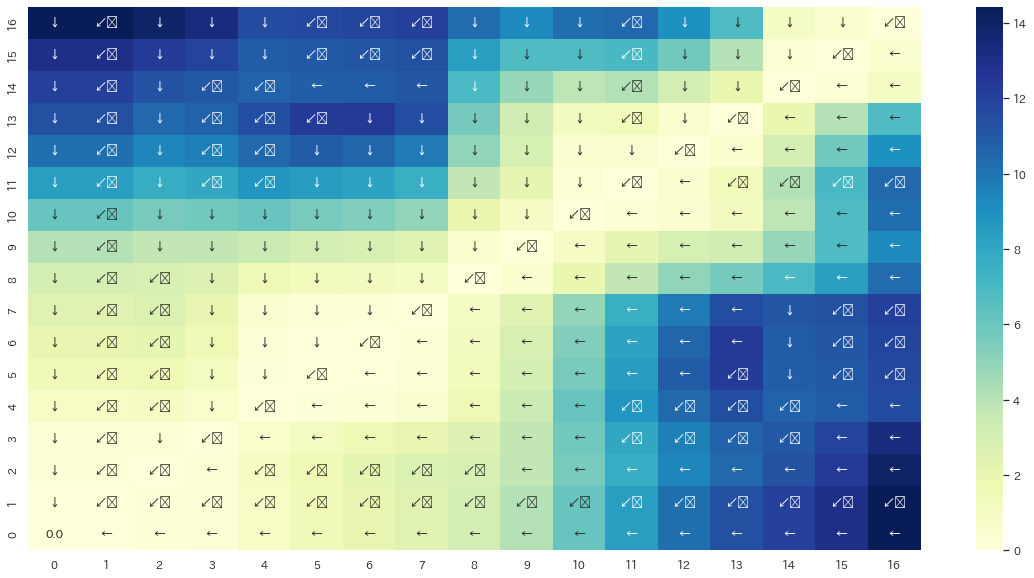
全く同じ波形を比較すれば、DDTWは0になるはずで、対角線上で常に「↙︎(=左下のマスが一番最小の値)」であるはずなのでそれを確認します。 行列を可視化するためにヒートマップを使用しています。
γ_mat, arrows, ddtw = DDTW(w2, w2)
sns.set(rc={"figure.figsize": (20, 10)})
sns.set(font="IPAexGothic")
ax = sns.heatmap(γ_mat, annot=True, fmt=".2f", cmap="YlGnBu")
ax.set_title(f"DDTW = {ddtw}")
ax.invert_yaxis()
ax.set_xlabel("w2")
ax.set_ylabel("w2")
plt.show()
ax = sns.heatmap(γ_mat, annot=arrows, fmt="", cmap="YlGnBu")
ax.invert_yaxis()
plt.show()
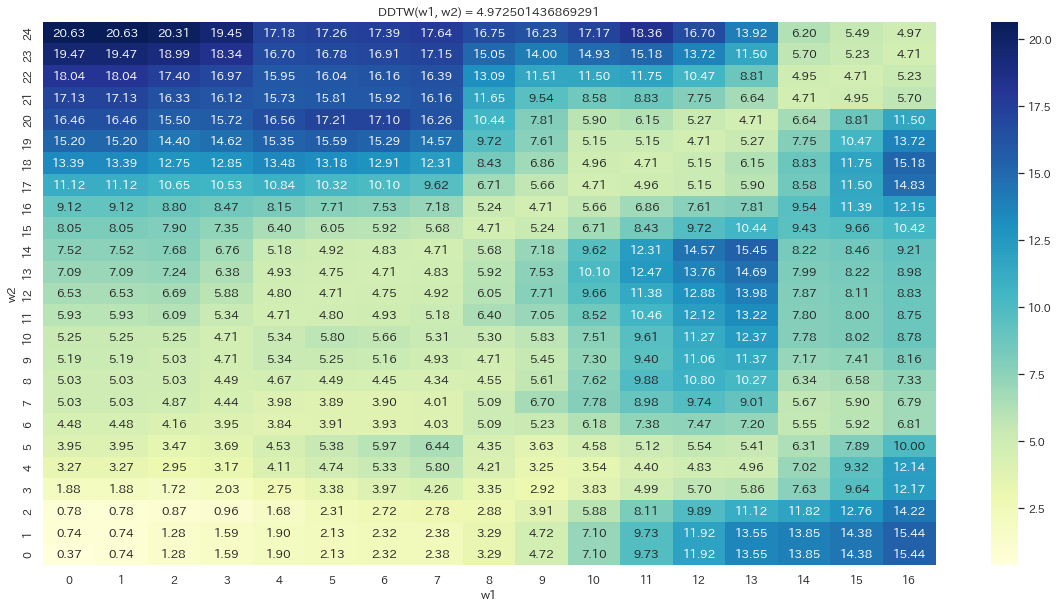
w2とw4のどちらがw1に近い形かDDTWで調べる
- w1 と w2は形が近いが、平均値が乖離している
- w2 と w4 は平均値が近いが、形が違う
ことが上のプロットでわかっているので、$DDTW(w_1, w_2) < DDTW(w_2, w_4)$ であってほしいです。
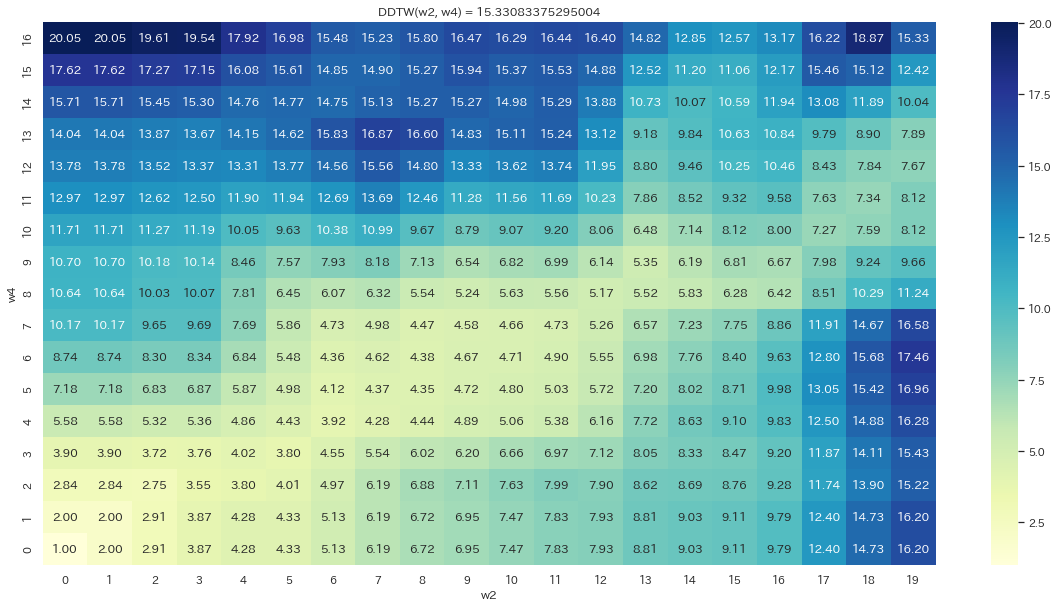
γ_mat, arrows, ddtw = DDTW(w2, w4)
sns.set(rc={"figure.figsize": (20, 10)})
sns.set(font="IPAexGothic")
ax = sns.heatmap(γ_mat, annot=True, fmt=".2f", cmap="YlGnBu")
ax.set_title(f"DDTW(w2, w4) = {ddtw}")
ax.invert_yaxis()
ax.set_xlabel("w2")
ax.set_ylabel("w4")
plt.show()
γ_mat, arrows, ddtw = DDTW(w1, w2)
sns.set(rc={"figure.figsize": (20, 10)})
sns.set(font="IPAexGothic")
ax = sns.heatmap(γ_mat, annot=True, fmt=".2f", cmap="YlGnBu")
ax.set_title(f"DDTW(w1, w2) = {ddtw}")
ax.invert_yaxis()
ax.set_xlabel("w1")
ax.set_ylabel("w2")
plt.show()