3.3.2
Box-Cox変換
まとめ
- 正の値を持つ特徴量の歪度を抑え、分布を正規分布に近づけるパワー変換を行う。
scipy.stats.boxcoxで変換し、boxcox_normmaxで最適な λ を最尤推定する。- 線形モデルや距離ベースの手法に渡す前に、歪んだ正の値の分布を対称化したいときに使う。
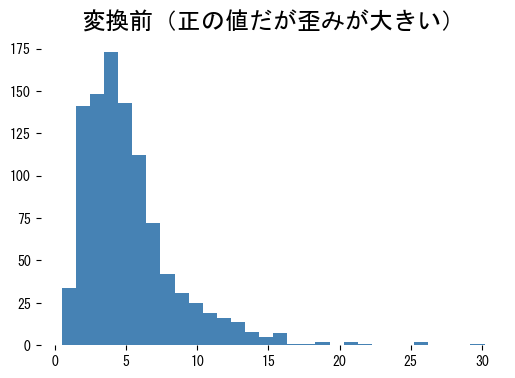
<p><b>Box-Cox変換</b>は、すべての観測値が正のときに歪度を抑え、分散を安定させるためのパワー変換です。ゼロや負の値が含まれる場合はデータを定数でシフトするか、Yeo-Johnson 変換への切り替えを検討します。</p>
定義 #
正の観測値 (x > 0) とパラメーター (\lambda) に対して Box-Cox 変換 (T_\lambda(x)) は
$$ T_\lambda(x) = \begin{cases} \dfrac{x^\lambda - 1}{\lambda}, & \lambda \ne 0,\\\\ \log x, & \lambda = 0. \end{cases} $$- (\lambda = 1) ならば値はそのまま、(\lambda = 0) では自然対数になります。
- 逆変換は
scipy.special.inv_boxcoxとして提供されています。 - (\lambda) の最尤推定は
scipy.stats.boxcox_normmaxで求められます。
式に (x^\lambda) と (\log x) が含まれるため、入力は必ず正の値に制限されます。必要に応じて小さな正の定数を加えてください。
実装例 #
| |
| |
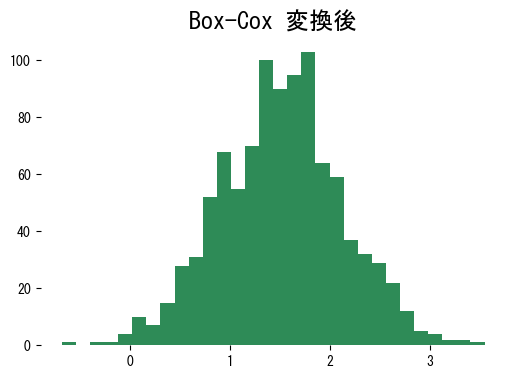
変換後の分布は左右対称に近づき、線形モデルや距離ベースの手法が扱いやすい形になります。
実務でのヒント #
- (\lambda) は学習データで推定し、検証・テストでも同じ値を再利用して情報漏洩を防ぎます。
- 予測結果を元のスケールに戻したい場合は
inv_boxcoxを利用します。 - モデルが平均 0・分散 1 を要求するなら、Box-Cox の後に
StandardScalerなどを組み合わせると安定します。 - 入力に 0 や負の値が含まれるときは Yeo-Johnson 変換か、定数シフトを検討してください。