3.3.2
StandardScaler で平均0・分散1に正規化する
まとめ- 各特徴量を平均 0・分散 1 の z スコアに標準化する。
sklearn.preprocessing.StandardScaler の fit_transform で変換し、inverse_transform で元のスケールに戻す。- SVM・k-NN・ロジスティック回帰など、距離や内積を利用するモデルの前処理として使う。
<p><b>StandardScaler</b> は各特徴量から平均を引き、標準偏差で割ることで平均 0・分散 1 のスケールに揃えます。距離や内積を利用する SVM、k-NN、ロジスティック回帰などでよく用いられる基本的な前処理です。</p>
定義
#
特徴量 (x) を平均 (\mu)、標準偏差 (\sigma) で正規化すると
$$
z = \frac{x - \mu}{\sigma}
$$となります。with_mean=False で中心化のみ、with_std=False でスケーリングのみを選択できます。
実装例
#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
rng = np.random.default_rng(21)
data = rng.normal(loc=[170, 65], scale=[8, 12], size=(500, 2))
scaler = StandardScaler()
scaled = scaler.fit_transform(data)
fig, axes = plt.subplots(1, 2, figsize=(10, 4))
axes[0].scatter(data[:, 0], data[:, 1], alpha=0.4, color="royalblue", edgecolor="none")
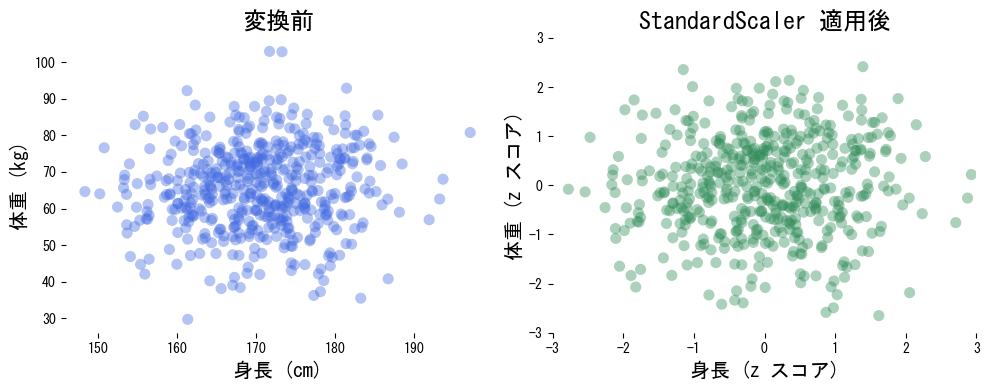
axes[0].set_title("変換前")
axes[0].set_xlabel("身長 (cm)")
axes[0].set_ylabel("体重 (kg)")
axes[1].scatter(scaled[:, 0], scaled[:, 1], alpha=0.4, color="seagreen", edgecolor="none")
axes[1].set_title("StandardScaler 適用後")
axes[1].set_xlabel("身長 (z スコア)")
axes[1].set_ylabel("体重 (z スコア)")
axes[1].set_xlim(-3, 3)
axes[1].set_ylim(-3, 3)
plt.tight_layout()
plt.show()
|
実務でのポイント
#
scaler.mean_ と scaler.scale_ を保存し、推論時も同じ scaler インスタンスで transform することで情報漏洩を防ぎます。- 元のスケールに戻したいときは
scaler.inverse_transform を利用します。 - 疎行列を扱う場合は
with_mean=False を指定し、計算コストとスパース性を維持するのが無難です。 - 外れ値が多い場合は先にロバストなスケーリングを行ってから StandardScaler を適用すると安定します。