Yeo-Johnson変換

最終更新 2025-11-03 読了時間 2 分

まとめ

0 や負の値を含む特徴量にも適用できるパワー変換で、分布を正規分布に近づける。
scipy.stats.yeojohnson で変換し、yeojohnson_normmax で最適な λ を最尤推定する。
Box-Cox 変換が使えない（負の値やゼロを含む）データの歪度補正が必要なときに使う。

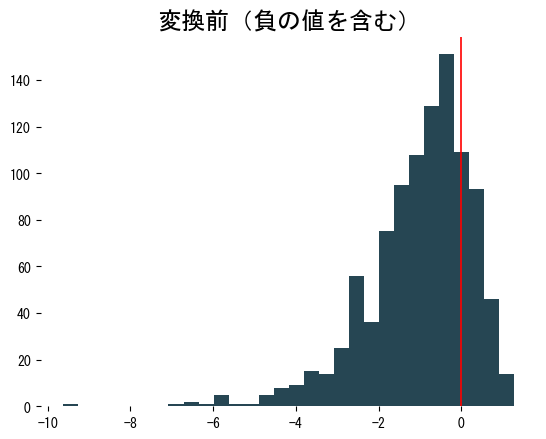
<p><b>Yeo-Johnson変換</b>は、数値データを正規分布に近づけるためのパワー変換です。Box-Cox変換を拡張した手法であり、<em>0 や負の値を含む特徴量にも</em>適用できる点が大きな特徴です。</p>

scipy.stats.yeojohnson

定義 #

観測値 (y) とパラメーター (\lambda) に対して、Yeo-Johnson変換 (T_\lambda(y)) は次のように定義されます。

$$ T_\lambda(y)= \begin{cases} \dfrac{(y + 1)^\lambda - 1}{\lambda}, & y \ge 0,\ \lambda \ne 0,\\\\ \log(y + 1), & y \ge 0,\ \lambda = 0,\\\\ -\dfrac{(1 - y)^{2 - \lambda} - 1}{2 - \lambda}, & y < 0,\ \lambda \ne 2,\\\\ -\log(1 - y), & y < 0,\ \lambda = 2. \end{cases} $$

(\lambda = 1) のときは元の値がそのまま返ります。
正の領域は (y+1) に対する Box-Cox 変換と同じ形になります。
負の領域ではデータを 0 を挟んで反転させることで、符号が変わる場合でも単調性が保たれます。
逆変換は同じ場合分けを (y) について解くことで得られ、SciPy では scipy.stats.yeojohnson_inverse が実装されています。

パラメーター (\lambda) は、変換後のデータが正規分布に従うと仮定した対数尤度を最大化することで推定するのが一般的です。SciPy にはこの推定量を返す yeojohnson_normmax が用意されています。

I. Yeo and R.A. Johnson, “A New Family of Power Transformations to Improve Normality or Symmetry”, Biometrika 87(4), 2000.

実装例 #

1
2
3
4
5
6
7
8
9
from scipy import stats
import matplotlib.pyplot as plt

# 負の値を含む歪んだ分布を作成
x = stats.loggamma.rvs(1, size=1_000) - 0.5
plt.hist(x, bins=30)
plt.axvline(x=0, color="r")
plt.title("変換前（負の値を含む）")
plt.show()

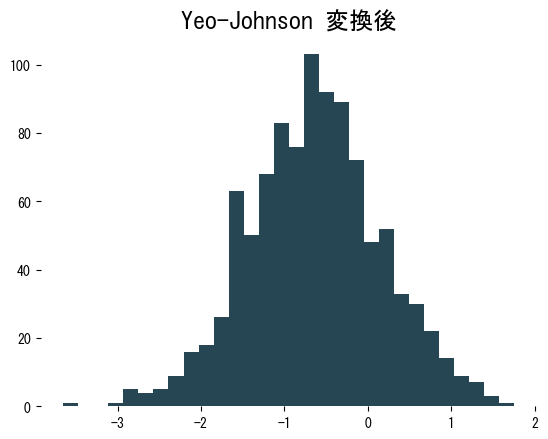
実装例の図

1
2
3
4
5
6
7
8
9
from scipy.stats import yeojohnson, yeojohnson_normmax

lmbda = yeojohnson_normmax(x)  # λ の最尤推定
print(f"推定された λ: {lmbda:.3f}")

x_trans = yeojohnson(x, lmbda=lmbda)
plt.hist(x_trans, bins=30)
plt.title("Yeo-Johnson 変換後")
plt.show()

実装例の図

変換後のヒストグラムは左右対称に近づき、分散も安定します。学習データで得た (\lambda) は、必ず検証・テストデータにも再利用してください。

1
2
X_train_trans = yeojohnson(X_train, lmbda=lmbda)
X_valid_trans = yeojohnson(X_valid, lmbda=lmbda)  # 学習データと同じ λ を使用

実務でのヒント #

変換後に平均 0・分散 1 を要求するモデルでは、StandardScaler などのスケーラーと組み合わせると安定します。
λ の推定は学習用データのみで行い、他の分割に漏らさないことで情報漏洩を防ぎます。
外れ値の影響が残る場合は RobustScaler などのロバストなスケーリングと併用することも検討しましょう。

Yeo-Johnson 変換は、正の値に限定される Box-Cox の代わりとして前処理パイプラインに簡単に組み込むことができます。