การตรวจจับความผิดปกติ ①

สัญชาตญาณ #

การตรวจจับความผิดปกติ ① ควรเข้าใจผ่านสมมติฐาน กลไกการปรับปรุงโมเดล และรูปแบบความผิดพลาดบนข้อมูลจริง เพื่อให้เลือกโมเดลและปรับพารามิเตอร์ได้อย่างเหมาะสม.

คำอธิบายโดยละเอียด #

1. เตรียมข้อมูลทดลอง #

ในตัวอย่างนี้ใช้ข้อมูลจาก Numenta Anomaly Benchmark (NAB)
และทดลองด้วย ADTK (Anomaly Detection Toolkit)

import pandas as pd
from adtk.data import validate_series

s_train = pd.read_csv(
    "./training.csv", index_col="timestamp", parse_dates=True, squeeze=True
)
s_train = validate_series(s_train)
print(s_train.head())

from adtk.visualization import plot
plot(s_train)

2. วิธีตรวจจับที่ใช้บ่อย #

ADTK มีตัวตรวจจับหลายแบบ ที่นี่เลือก 5 วิธีหลักมาเปรียบเทียบ

import matplotlib.pyplot as plt
from adtk.detector import (
    AutoregressionAD,
    InterQuartileRangeAD,
    LevelShiftAD,
    PersistAD,
    SeasonalAD,
)

model_dict = {
    "LevelShiftAD": LevelShiftAD(window=5),
    "SeasonalAD": SeasonalAD(),
    "PersistAD": PersistAD(c=3.0, side="positive"),
    "InterQuartileRangeAD": InterQuartileRangeAD(c=1.5),
    "AutoregressionAD": AutoregressionAD(n_steps=14, step_size=24, c=3.0),
}

for model_name, model in model_dict.items():
    anomalies = model.fit_detect(s_train)
    plot(s_train, anomaly=anomalies, anomaly_color="red", anomaly_tag="marker")
    plt.title(model_name)
    plt.show()

3. แนวคิดและสมการของแต่ละวิธี #

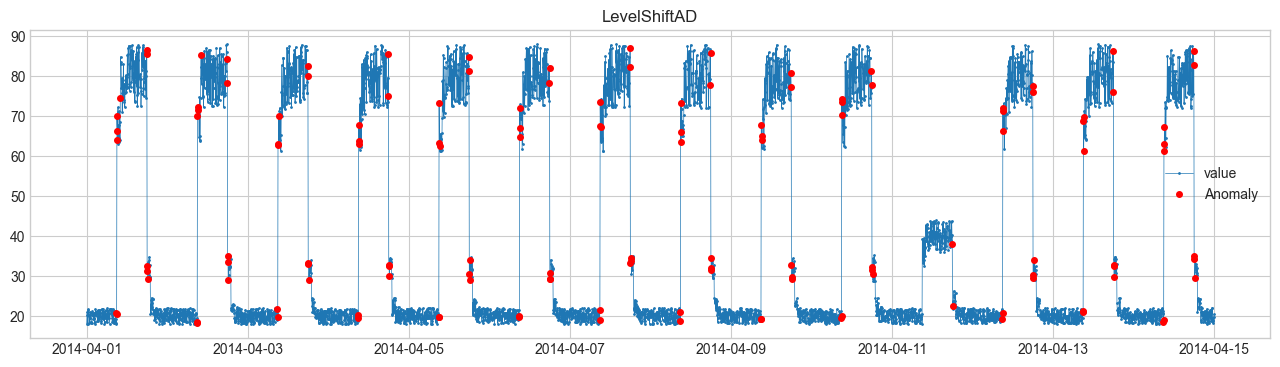
(1) LevelShiftAD (การเปลี่ยนระดับ) #

ตรวจว่าค่าเฉลี่ยเปลี่ยนฉับพลันหรือไม่
เช่น ค่าเซนเซอร์กระโดดขึ้นหรือลงแบบทันที

ถ้า \(|\Delta_t|\) ใหญ่พอ → ถือเป็นความผิดปกติ

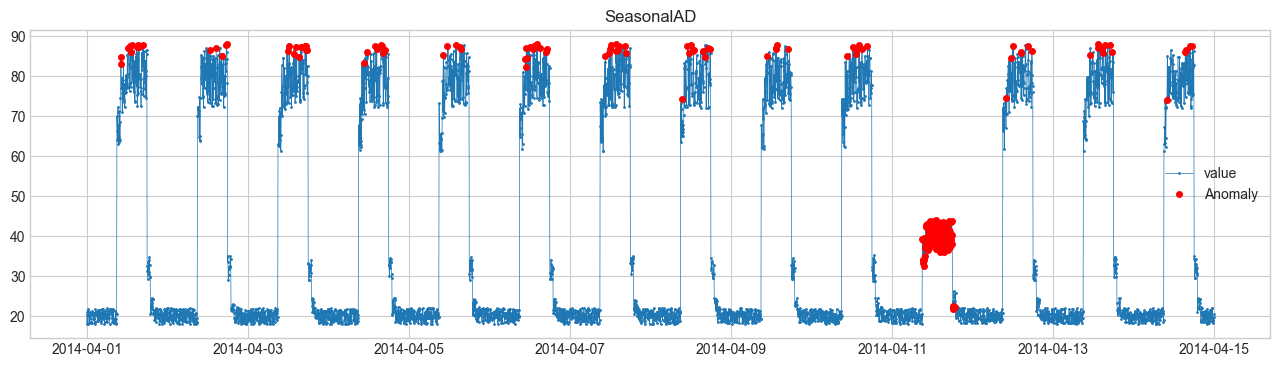
(2) SeasonalAD (เบี่ยงจากฤดูกาล) #

เรียนรู้รูปแบบตามคาบ แล้วตรวจจุดที่เบี่ยงจากรูปแบบนั้น
เช่น จำนวนผู้ใช้งานรายวันที่พุ่งสูงผิดปกติ

ถ้า \(e_t\) ใหญ่ → ผิดปกติ

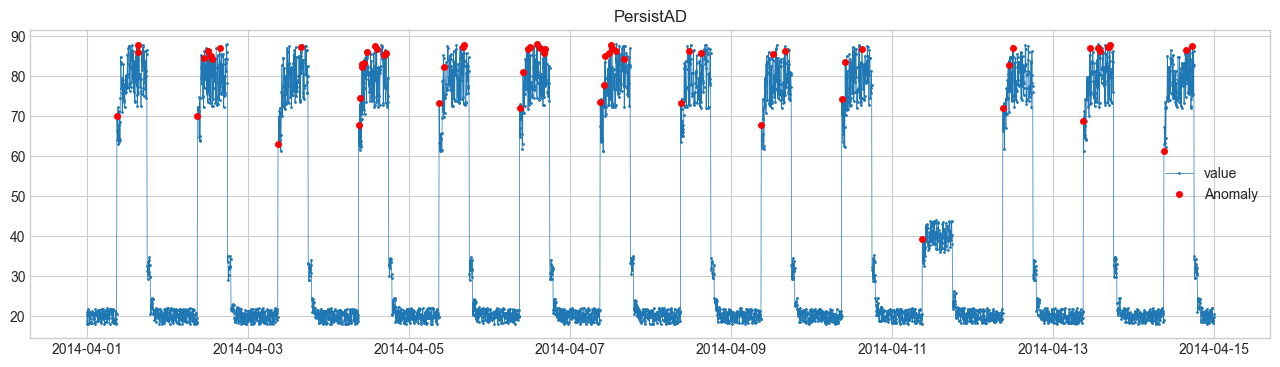
(3) PersistAD (ค่าคงค้างผิดปกติ) #

ดูว่าแตกต่างจากค่าก่อนหน้ามากเกินไปหรือไม่

ถ้าเกิน \(c\) → ผิดปกติ

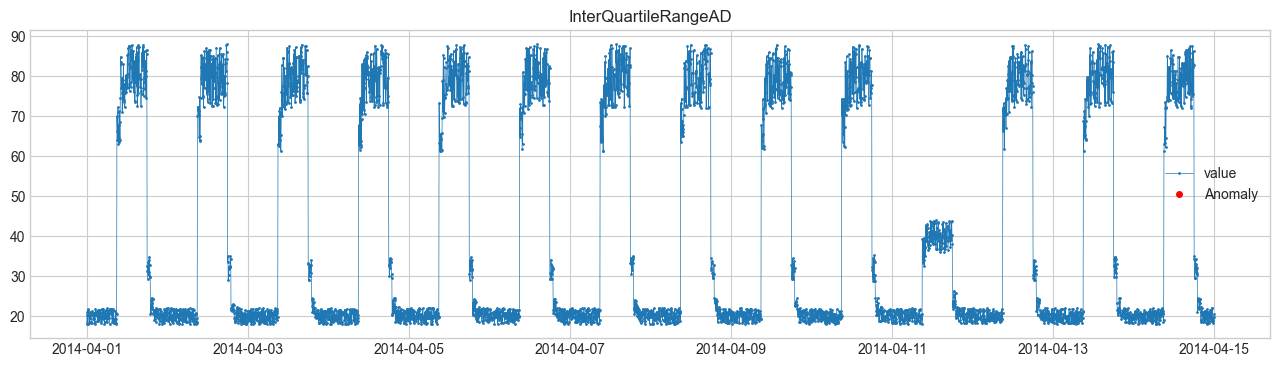
(4) InterQuartileRangeAD (ช่วงควอไทล์) #

ตรวจ outlier ด้วยสถิติ
ใช้ควอไทล์ที่ 1 \(Q1\), ควอไทล์ที่ 3 \(Q3\) และช่วงควอไทล์ \(IQR=Q3-Q1\)

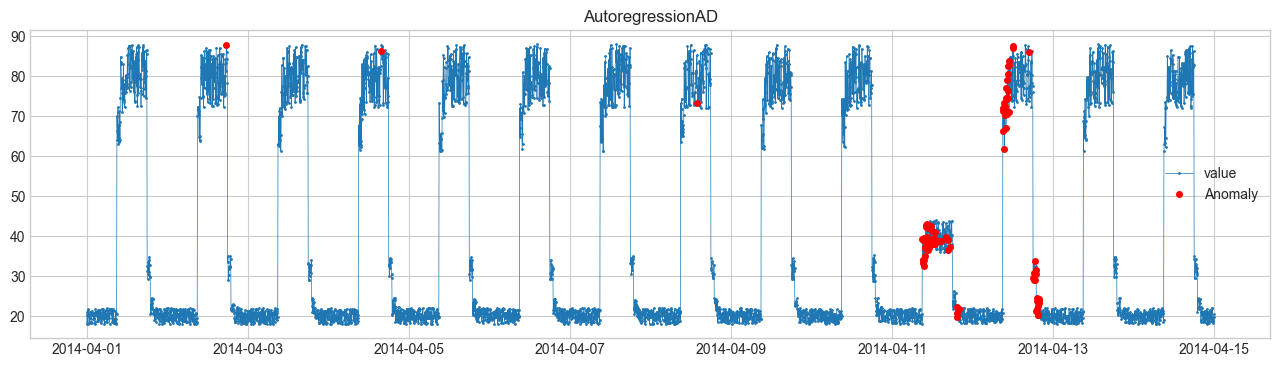
(5) AutoregressionAD (ออโตเรเกรสชัน) #

พยากรณ์อนาคตจากอดีต แล้วดูค่าคลาดเคลื่อน

ถ้าเศษเหลือ \(\epsilon_t\) ใหญ่ → ผิดปกติ

4. ผลการแสดงผล #