2.1.6
การถดถอยเชิงเส้นแบบเบย์
สรุป
- การถดถอยเชิงเส้นแบบเบย์มองค่าสัมประสิทธิ์เป็นตัวแปรสุ่ม จึงประมาณได้ทั้งค่าคาดหวังและความไม่แน่นอนของผลพยากรณ์พร้อมกัน
- สามารถหาส่วนกระจายภายหลังได้แบบปิดรูปจากข้อมูลและการแจกแจงล่วงหน้า ทำให้ทำงานได้ทนทานแม้ข้อมูลมีค่าผิดปกติหรือมีปริมาณน้อย
- การแจกแจงพยากรณ์เป็นแบบแกาสเซียน จึงแสดงค่าเฉลี่ยและช่วงความเชื่อมั่นเพื่อช่วยการตัดสินใจได้ง่าย
- ใน
scikit-learnใช้BayesianRidgeก็จะประมาณความแปรปรวนของสัญญาณและของสัญญาณรบกวนให้อัตโนมัติ เหมาะกับงานจริง
สัญชาตญาณ #
การเข้าใจวิธีนี้ควรดูสมมติฐานของโมเดล ลักษณะข้อมูล และผลของการตั้งค่าพารามิเตอร์ต่อการทั่วไปของโมเดล
คำอธิบายโดยละเอียด #
สูตรสำคัญ #
ให้เวกเตอร์สัมประสิทธิ์ \(\boldsymbol\beta\) มีการแจกแจงก่อนหน้าเป็นแกาสเซียนหลายมิติที่มีค่าเฉลี่ยศูนย์และความแปรปรวนร่วม \(\tau^{-1}\mathbf{I}\) และสมมติสัญญาณรบกวน \(\epsilon_i \sim \mathcal{N}(0, \alpha^{-1})\) จะได้การแจกแจงภายหลัง
$$ p(\boldsymbol\beta \mid \mathbf{X}, \mathbf{y}) = \mathcal{N}(\boldsymbol\beta \mid \boldsymbol\mu, \mathbf{\Sigma}) $$โดยมี
$$ \mathbf{\Sigma} = (\alpha \mathbf{X}^\top \mathbf{X} + \tau \mathbf{I})^{-1}, \qquad \boldsymbol\mu = \alpha \mathbf{\Sigma} \mathbf{X}^\top \mathbf{y} $$เมื่อได้เวกเตอร์ใหม่ \(\mathbf{x}*\) การแจกแจงของคำตอบก็ยังเป็นแกาสเซียน \(\mathcal{N}(\hat{y}, \sigma_^2)\) เช่นเดิม BayesianRidge ใน scikit-learn จะประมาณ \(\alpha\) และ \(\tau\) จากข้อมูลให้ด้วย จึงใช้งานกรอบนี้ได้สะดวก
ทดลองด้วย Python #
ตัวอย่างด้านล่างใช้ข้อมูลเส้นตรงที่มี noise และ outlier เพื่อเปรียบเทียบระหว่างการถดถอยเชิงเส้นแบบกำลังสองน้อยที่สุดกับการถดถอยแบบเบย์
from __future__ import annotations
import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import BayesianRidge, LinearRegression
from sklearn.metrics import mean_squared_error
def run_bayesian_linear_demo(
n_samples: int = 120,
noise_scale: float = 1.0,
outlier_count: int = 6,
outlier_scale: float = 8.0,
label_observations: str = "observations",
label_ols: str = "OLS",
label_bayes: str = "Bayesian mean",
label_interval: str = "95% CI",
xlabel: str = "input $",
ylabel: str = "output $",
title: str | None = None,
) -> dict[str, float]:
"""Fit OLS and Bayesian ridge to noisy data with outliers, plotting results.
Args:
n_samples: Number of evenly spaced sample points.
noise_scale: Standard deviation of Gaussian noise added to the base line.
outlier_count: Number of indices to perturb strongly.
outlier_scale: Standard deviation for the outlier noise.
label_observations: Legend label for observations.
label_ols: Label for the ordinary least squares line.
label_bayes: Label for the Bayesian posterior mean line.
label_interval: Label for the confidence interval band.
xlabel: X-axis label.
ylabel: Y-axis label.
title: Optional plot title.
Returns:
Dictionary containing MSEs and coefficients statistics.
"""
japanize_matplotlib.japanize()
rng = np.random.default_rng(seed=0)
x_values: np.ndarray = np.linspace(-4.0, 4.0, n_samples, dtype=float)
y_clean: np.ndarray = 1.8 * x_values - 0.5
y_noisy: np.ndarray = y_clean + rng.normal(scale=noise_scale, size=x_values.shape)
outlier_idx = rng.choice(n_samples, size=outlier_count, replace=False)
y_noisy[outlier_idx] += rng.normal(scale=outlier_scale, size=outlier_idx.shape)
X: np.ndarray = x_values[:, np.newaxis]
ols = LinearRegression()
ols.fit(X, y_noisy)
bayes = BayesianRidge(compute_score=True)
bayes.fit(X, y_noisy)
X_grid: np.ndarray = np.linspace(-6.0, 6.0, 200, dtype=float)[:, np.newaxis]
ols_mean: np.ndarray = ols.predict(X_grid)
bayes_mean, bayes_std = bayes.predict(X_grid, return_std=True)
metrics = {
"ols_mse": float(mean_squared_error(y_noisy, ols.predict(X))),
"bayes_mse": float(mean_squared_error(y_noisy, bayes.predict(X))),
"coef_mean": float(bayes.coef_[0]),
"coef_std": float(np.sqrt(bayes.sigma_[0, 0])),
}
upper = bayes_mean + 1.96 * bayes_std
lower = bayes_mean - 1.96 * bayes_std
fig, ax = plt.subplots(figsize=(10, 5))
ax.scatter(X, y_noisy, color="#ff7f0e", alpha=0.6, label=label_observations)
ax.plot(X_grid, ols_mean, color="#1f77b4", linestyle="--", label=label_ols)
ax.plot(X_grid, bayes_mean, color="#2ca02c", linewidth=2, label=label_bayes)
ax.fill_between(
X_grid.ravel(),
lower,
upper,
color="#2ca02c",
alpha=0.2,
label=label_interval,
)
ax.set_xlabel(xlabel)
ax.set_ylabel(ylabel)
if title:
ax.set_title(title)
ax.legend()
fig.tight_layout()
plt.show()
return metrics
metrics = run_bayesian_linear_demo(
label_observations="ข้อมูลที่สังเกต",
label_ols="เส้น OLS",
label_bayes="ค่าเฉลี่ยแบบเบย์",
label_interval="ช่วงความเชื่อมั่น 95%",
xlabel="อินพุต $x$",
ylabel="เอาต์พุต $y$",
title="เปรียบเทียบ OLS กับการถดถอยแบบเบย์",
)
print(f"MSE ของ OLS: {metrics['ols_mse']:.3f}")
print(f"MSE ของเบย์: {metrics['bayes_mse']:.3f}")
print(f"ค่าเฉลี่ยภายหลังของสัมประสิทธิ์: {metrics['coef_mean']:.3f}")
print(f"ส่วนเบี่ยงเบนมาตรฐานภายหลัง: {metrics['coef_std']:.3f}")
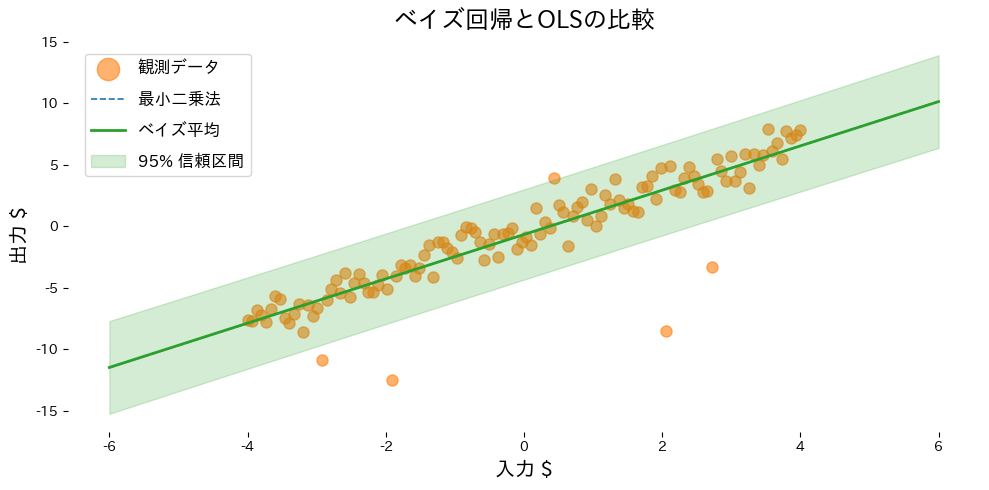
วิเคราะห์ผลลัพธ์ #
- OLS ถูกดึงให้เอียงตาม outlier ได้ง่าย ในขณะที่แบบเบย์สามารถหาค่าเฉลี่ยที่เสถียรกว่า
- เมื่อใช้
return_std=Trueจะได้ส่วนเบี่ยงเบนมาตรฐานของการพยากรณ์ จึงวาดช่วงความเชื่อมั่นได้ทันที - ตรวจสอบความแปรปรวนภายหลังของสัมประสิทธิ์เพื่อดูว่าคุณสมบัติใดยังมีความไม่แน่นอนอยู่มาก
เอกสารอ้างอิง #
- Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.
- Murphy, K. P. (2012). Machine Learning: A Probabilistic Perspective. MIT Press.