2.1.1
การถดถอยเชิงเส้น
สรุป
- การถดถอยเชิงเส้นเป็นแบบจำลองพื้นฐานที่สรุปความสัมพันธ์เชิงเส้นระหว่างอินพุตกับเอาต์พุต ใช้ได้ทั้งเพื่อพยากรณ์และตีความ
- วิธีการกำลังสองน้อยที่สุดประมาณสัมประสิทธิ์ด้วยการทำให้ผลรวมกำลังสองของค่าคลาดเคลื่อนต่ำสุด จึงมีคำตอบแบบปิดรูปและเข้าใจกลไกได้ง่าย
- สัมประสิทธิ์ความชันบอกว่า “เมื่ออินพุตเพิ่ม 1 หน่วย เอาต์พุตจะเปลี่ยนเท่าไร” ส่วนค่าตัดแกนบอกค่าเฉลี่ยเมื่ออินพุตเป็นศูนย์
- เมื่อนอยส์หรือ outlier สูง ควรพิจารณาทำมาตรฐานหรือใช้วิธีที่ทนทาน พร้อมตรวจสอบขั้นตอนก่อนประมวลผลและการประเมินผลร่วมกัน
สัญชาตญาณ #
การเข้าใจวิธีนี้ควรดูสมมติฐานของโมเดล ลักษณะข้อมูล และผลของการตั้งค่าพารามิเตอร์ต่อการทั่วไปของโมเดล
คำอธิบายโดยละเอียด #
สูตรสำคัญ #
แบบจำลองเชิงเส้นอันดับหนึ่งเขียนได้เป็น
$$ y = w x + b $$ให้ผลต่างระหว่างค่าจริงกับค่าพยากรณ์เป็น \(\epsilon_i = y_i - (w x_i + b)\) แล้วนิยามฟังก์ชันวัตถุประสงค์
$$ L(w, b) = \sum_{i=1}^{n} \big(y_i - (w x_i + b)\big)^2 $$การทำให้ \(L\) ต่ำสุดให้คำตอบปิดรูป
$$ w = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2}, \qquad b = \bar{y} - w \bar{x} $$โดย \(\bar{x}, \bar{y}\) คือค่าเฉลี่ยของข้อมูล การถดถอยพหุคูณก็ขยายแนวคิดเดียวกันด้วยเมทริกซ์และเวกเตอร์
ทดลองด้วย Python #
โค้ดด้านล่างใช้ scikit-learn สร้างข้อมูลสังเคราะห์ เทรนแบบจำลอง และวาดเส้นที่ประมาณได้
from __future__ import annotations
import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
def plot_simple_linear_regression(n_samples: int = 100) -> None:
"""Plot a fitted linear regression model for synthetic data.
Args:
n_samples: Number of synthetic samples to generate.
"""
japanize_matplotlib.japanize()
rng = np.random.default_rng(seed=0)
X: np.ndarray = np.linspace(-5.0, 5.0, n_samples, dtype=float)[:, np.newaxis]
noise: np.ndarray = rng.normal(scale=2.0, size=n_samples)
y: np.ndarray = 2.0 * X.ravel() + 1.0 + noise
model = make_pipeline(StandardScaler(with_mean=False), LinearRegression())
model.fit(X, y)
y_pred: np.ndarray = model.predict(X)
fig, ax = plt.subplots(figsize=(10, 5))
ax.scatter(X, y, marker="x", label="ข้อมูลจริง", c="orange")
ax.plot(X, y_pred, label="ผลพยากรณ์เชิงเส้น")
ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
ax.legend()
fig.tight_layout()
plt.show()
plot_simple_linear_regression()
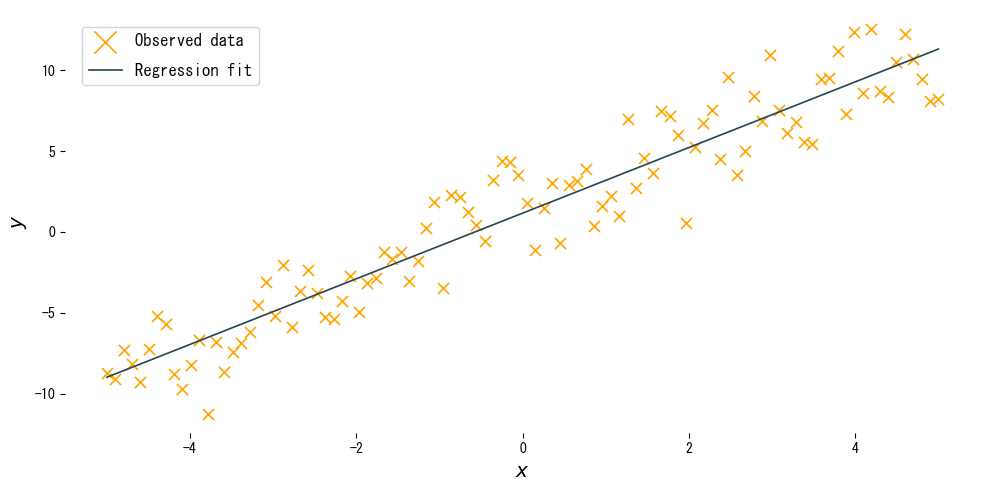
วิเคราะห์ผลลัพธ์ #
- ความชัน \(w\) ระบุว่าเมื่ออินพุตเพิ่ม 1 หน่วย เอาต์พุตจะเพิ่มหรือลดเท่าไร และควรเข้าใกล้ความชันจริงของข้อมูล
- ค่าตัดแกน \(b\) คือค่าเฉลี่ยของเอาต์พุตเมื่ออินพุตเป็นศูนย์ ใช้ขยับเส้นขึ้นหรือลง
- การทำมาตรฐานด้วย
StandardScalerช่วยให้เรียนรู้ได้เสถียรแม้อินพุตอยู่คนละสเกล
เอกสารอ้างอิง #
- Draper, N. R., & Smith, H. (1998). Applied Regression Analysis (3rd ed.). John Wiley & Sons.
- Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning. Springer.