2.1.8
PCR
สรุป
- PCR ทำ PCA เพื่อลดมิติก่อน แล้วค่อยถดถอยเชิงเส้น ลดความไม่เสถียรที่เกิดจากตัวแปรอธิบายมีความสัมพันธ์กันสูง
- PCA เน้นทิศทางที่มีความแปรปรวนสูง จึงตัดแกนที่มี noise มากและรักษาข้อมูลสำคัญไว้ได้
- การเลือกจำนวนองค์ประกอบที่เก็บไว้ช่วยป้องกัน overfitting และยังลดภาระการคำนวณ
- การเตรียมข้อมูล เช่น การทำมาตรฐานและจัดการค่าหาย เป็นพื้นฐานสำคัญสำหรับความแม่นยำและการตีความ
สัญชาตญาณ #
การเข้าใจวิธีนี้ควรดูสมมติฐานของโมเดล ลักษณะข้อมูล และผลของการตั้งค่าพารามิเตอร์ต่อการทั่วไปของโมเดล
คำอธิบายโดยละเอียด #
สูตรสำคัญ #
หลังจากทำมาตรฐานเมทริกซ์ตัวอธิบาย \(\mathbf{X}\) แล้วใช้ PCA เพื่อเลือกองค์ประกอบ \(k\) ตัวที่มีค่าลักษณะเฉพาะสูงที่สุด เราจะได้คะแนน \(\mathbf{Z} = \mathbf{X}\mathbf{W}_k\) จากนั้นเรียนรู้โมเดล
$$ y = \boldsymbol{\gamma}^\top \mathbf{Z} + b $$ท้ายที่สุดสามารถแปลงกลับเป็นสัมประสิทธิ์บนฟีเจอร์เดิมด้วย \(\boldsymbol{\beta} = \mathbf{W}_k \boldsymbol{\gamma}\) จำนวนองค์ประกอบ \(k\) มักเลือกจากอัตราการอธิบายความแปรปรวนหรือ cross-validation
ทดลองด้วย Python #
ตัวอย่างต่อไปนี้ใช้ชุดข้อมูลโรคเบาหวานเพื่อดูผลของจำนวนองค์ประกอบต่างๆ ต่อค่า CV MSE
from __future__ import annotations
import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_diabetes
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
def evaluate_pcr_components(
cv_folds: int = 5,
xlabel: str = "Number of components k",
ylabel: str = "CV MSE (lower is better)",
title: str | None = None,
label_best: str = "best={k}",
) -> dict[str, float]:
"""Cross-validate PCR with varying component counts and plot the curve.
Args:
cv_folds: Number of folds for cross-validation.
xlabel: Label for the component-count axis.
ylabel: Label for the error axis.
title: Optional title for the plot.
label_best: Format string for highlighting the best component count.
Returns:
Dictionary containing the best component count and its CV score.
"""
japanize_matplotlib.japanize()
X, y = load_diabetes(return_X_y=True)
def build_pcr(n_components: int) -> Pipeline:
return Pipeline(
[
("scale", StandardScaler()),
("pca", PCA(n_components=n_components, random_state=0)),
("reg", LinearRegression()),
]
)
components = np.arange(1, X.shape[1] + 1)
cv_scores = []
for k in components:
model = build_pcr(int(k))
score = cross_val_score(
model,
X,
y,
cv=cv_folds,
scoring="neg_mean_squared_error",
)
cv_scores.append(score.mean())
cv_scores_arr = np.array(cv_scores)
best_idx = int(np.argmax(cv_scores_arr))
best_k = int(components[best_idx])
best_mse = float(-cv_scores_arr[best_idx])
best_model = build_pcr(best_k).fit(X, y)
explained = best_model["pca"].explained_variance_ratio_
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(components, -cv_scores_arr, marker="o")
ax.axvline(best_k, color="red", linestyle="--", label=label_best.format(k=best_k))
ax.set_xlabel(xlabel)
ax.set_ylabel(ylabel)
if title:
ax.set_title(title)
ax.legend()
fig.tight_layout()
plt.show()
return {
"best_k": best_k,
"best_mse": best_mse,
"explained_variance_ratio": explained,
}
metrics = evaluate_pcr_components(
xlabel="จำนวนองค์ประกอบ k",
ylabel="CV MSE (ยิ่งต่ำยิ่งดี)",
title="ผลของจำนวนองค์ประกอบใน PCR",
label_best="k ที่ดีที่สุด = {k}",
)
print(f"จำนวนองค์ประกอบที่เหมาะสม: {metrics['best_k']}")
print(f"ค่า CV MSE ที่ดีที่สุด: {metrics['best_mse']:.3f}")
print("สัดส่วนความแปรปรวนที่อธิบายได้:", metrics["explained_variance_ratio"])
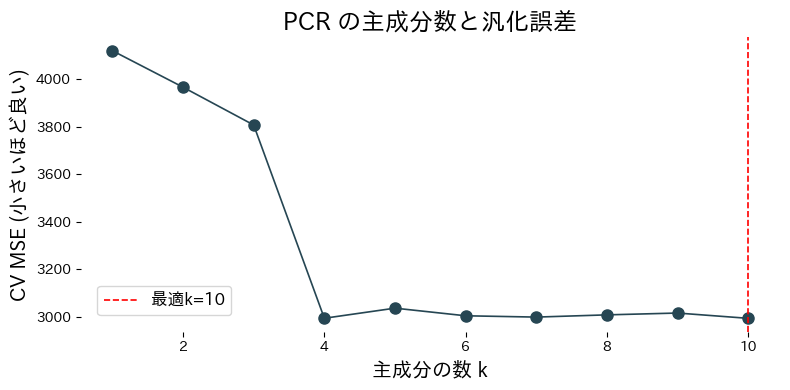
วิเคราะห์ผลลัพธ์ #
- เมื่อเพิ่มจำนวนองค์ประกอบ ค่า CV MSE จะลดลงจนถึงจุดที่ดีที่สุด จากนั้นเริ่มสูงขึ้นซึ่งบ่งชี้ถึง overfitting
- การดู
explained_variance_ratio_บอกได้ว่าองค์ประกอบใดมีผลต่อการอธิบายข้อมูลมากที่สุด - ตรวจสอบ loading ของ PCA เพื่อรู้ว่าฟีเจอร์ใดรวมตัวกันเป็นองค์ประกอบแต่ละตัว ช่วยตีความผลลัพธ์
เอกสารอ้างอิง #
- Jolliffe, I. T. (2002). Principal Component Analysis (2nd ed.). Springer.
- Massy, W. F. (1965). Principal Components Regression in Exploratory Statistical Research. Journal of the American Statistical Association, 60(309), 234 E56.