พารามิเตอร์ของ Decision Tree | ปรับความลึก ใบไม้ และการ pruning

1. ภาพรวม #

ต้นไม้จะขยายโดยเลือก split ที่ลดความไม่บริสุทธิ์ได้มากที่สุด หากไม่มีข้อจำกัด ต้นไม้มักโตจน overfit จึงต้องใช้พารามิเตอร์เป็นตัวควบคุม เช่น จำกัดความลึก กำหนดจำนวนตัวอย่างขั้นต่ำต่อใบ และทำ pruning เพื่อตัดกิ่งที่ไม่คุ้มค่า

2. Impurity gain และ cost-complexity pruning #

สำหรับโหนดพ่อ (P) ที่แบ่งเป็น (L) และ (R) การลด impurity คือ

$$ \Delta I = I(P) - \frac{|L|}{|P|} I(L) - \frac{|R|}{|P|} I(R), $$

โดย (I(\cdot)) อาจเป็น Gini, entropy, MSE หรือ MAE ตามงาน หาก (\Delta I \le 0) จะไม่เก็บ split

Cost-complexity pruning ให้คะแนนต้นไม้ทั้งต้น (T) เป็น

$$ R_\alpha(T) = R(T) + \alpha |T|, $$

ที่ (R(T)) คือ loss ของการฝึก, (|T|) คือจำนวนใบ และ (\alpha \ge 0) ใช้ลงโทษต้นไม้ใหญ่ ค่าที่สูงขึ้นทำให้ต้นไม้เรียบง่ายขึ้น

3. ทดลองด้วย Python #

โค้ดด้านล่างฝึก DecisionTreeRegressor หลายตัว และเปรียบเทียบ (R^2) ของ train/validation เพื่อเห็นผลของ max_depth, min_samples_leaf, และ ccp_alpha

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
from sklearn.datasets import make_regression
from sklearn.metrics import r2_score

X, y = make_regression(
    n_samples=500,
    n_features=2,
    noise=0.2,
    random_state=42,
)
Xtr, Xte, ytr, yte = train_test_split(X, y, test_size=0.3, random_state=0)

def evaluate(params):
    model = DecisionTreeRegressor(random_state=0, **params).fit(Xtr, ytr)
    r2_train = r2_score(ytr, model.predict(Xtr))
    r2_test = r2_score(yte, model.predict(Xte))
    print(f"{params}: train R2={r2_train:.3f}, test R2={r2_test:.3f}")

evaluate({"max_depth": 3})
evaluate({"max_depth": 10})
evaluate({"max_depth": 5, "min_samples_leaf": 5})
evaluate({"max_depth": 5, "ccp_alpha": 0.01})

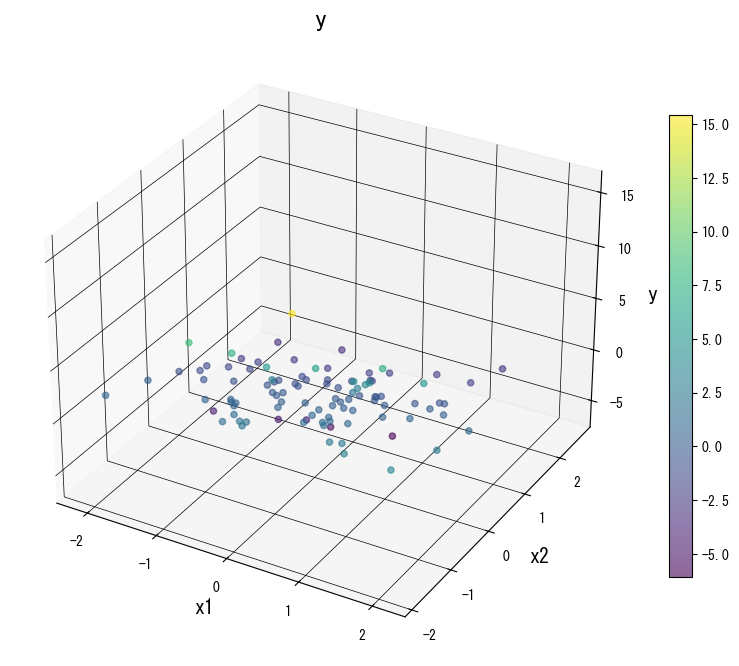
ภาพด้านล่าง (ใช้รูปเดียวกับหน้า JP) แสดงผลของการปรับพารามิเตอร์หลัก:

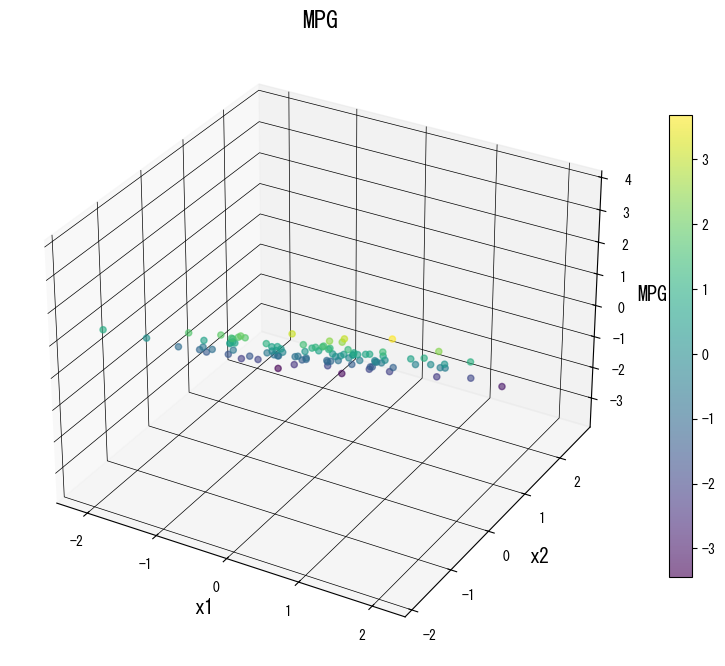
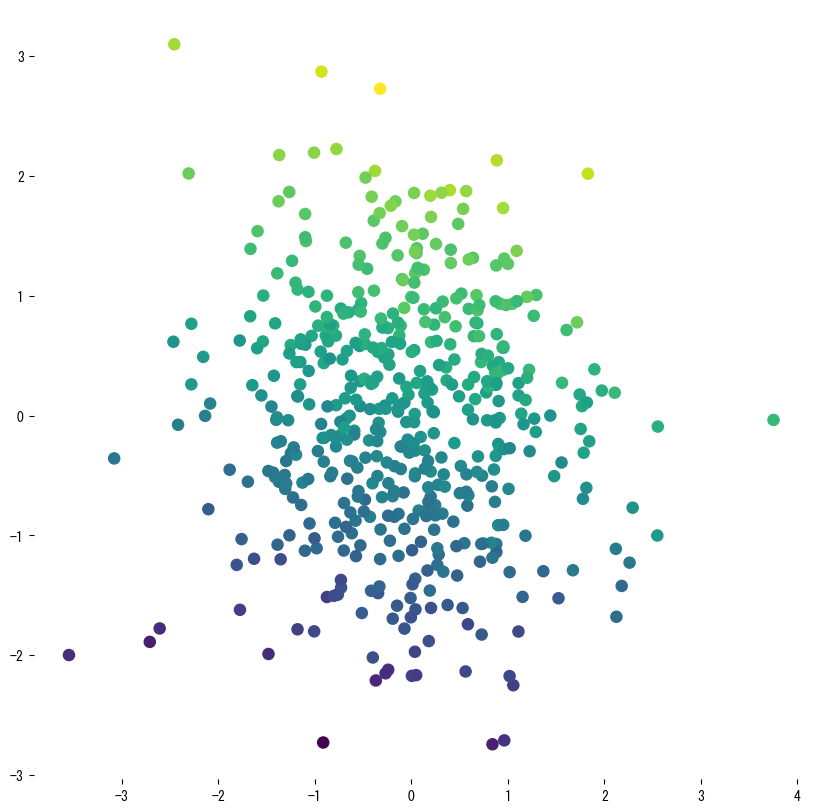
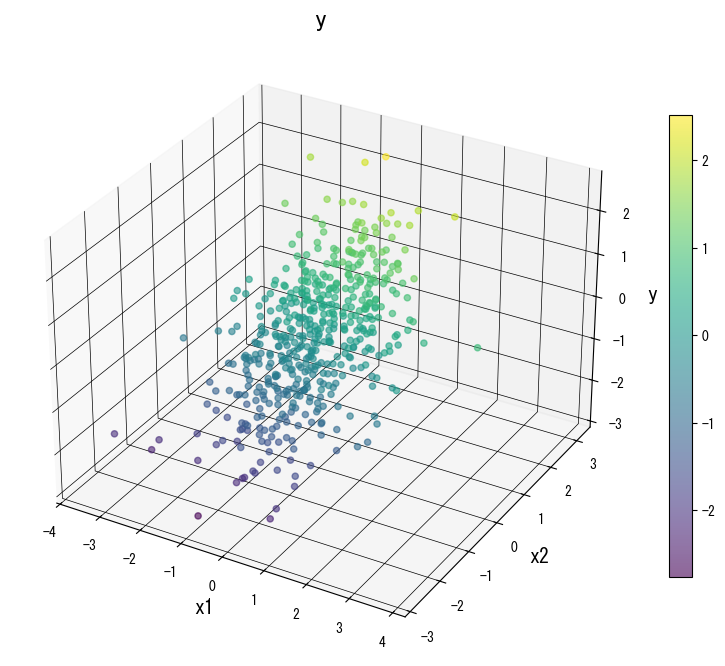
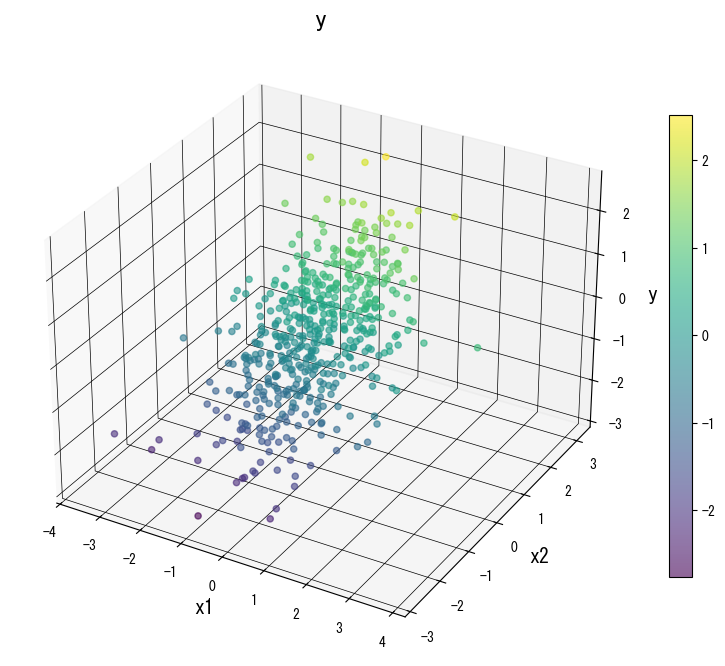
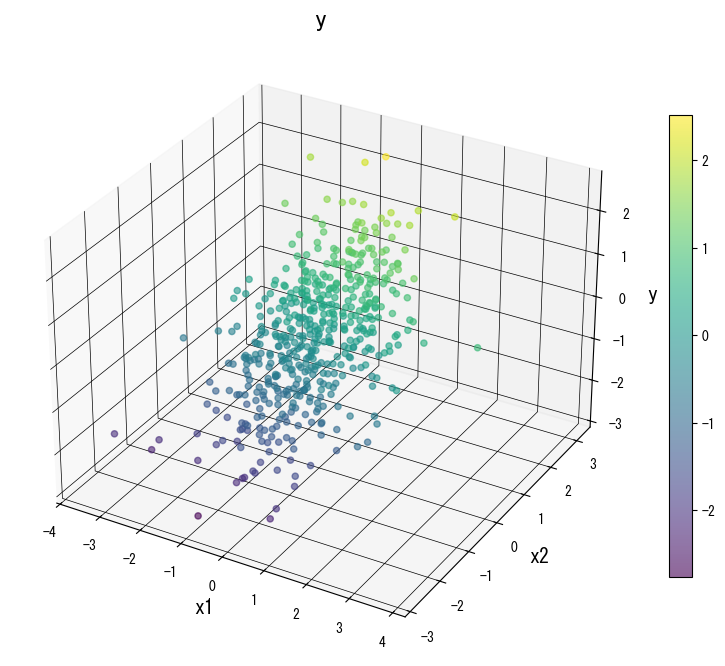
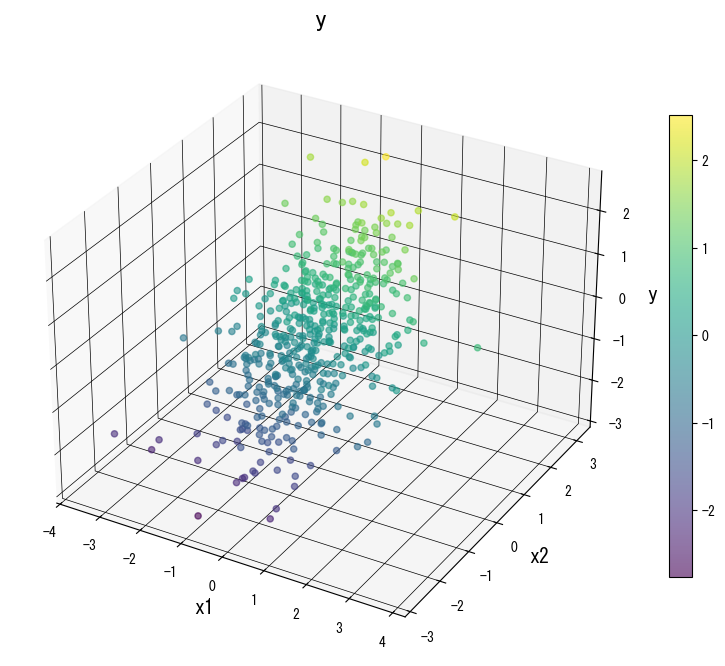
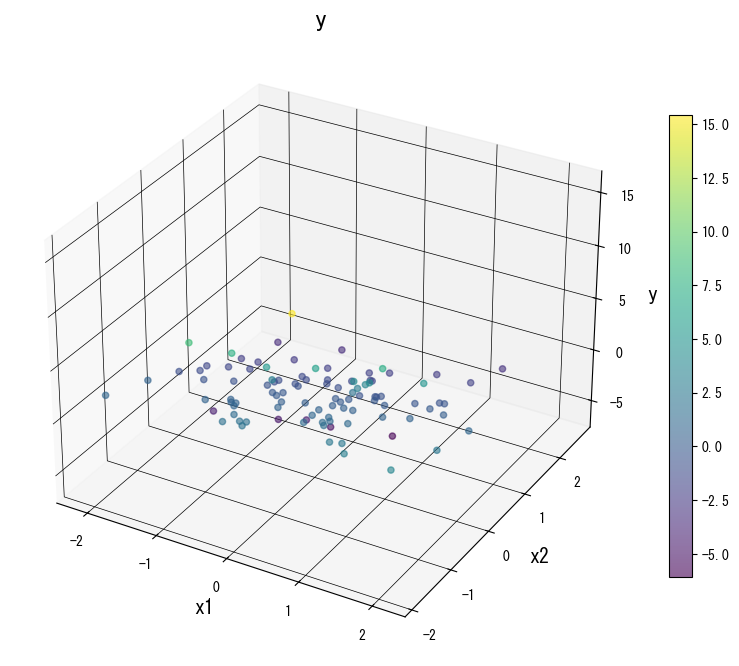
4. อ้างอิง #