まとめ- AR(自己回帰)過程は、過去の自分自身の値に依存する確率過程。
- 係数を変えたシミュレーションで、系列の振る舞い(定常・ランダムウォーク・発散)を確認する。
- AR(1)からAR(2)への拡張と、statsmodelsによるモデル推定を学ぶ。
ARモデルは自己回帰モデルとも呼ばれるものです。時点tにおけるモデルの出力は時点t以前の自分自身の出力に依存する確率過程のことを指しています。
1
2
3
| import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt
|
AR過程のデータを作成する
#
データを生成するための関数を用意します
1
2
3
4
5
6
7
8
9
10
11
12
| def create_ARdata(phis=[0.1], N=500, init=1, c=1, sigma=0.3):
"""AR過程のデータを作成する"""
print(f"==AR({len(phis)})過程の長さ{N}のデータを作成==")
data = np.zeros(N)
data[0] = init + np.random.normal(0, sigma)
for t in range(2, N):
res = c + np.random.normal(0, sigma)
for j, phi_j in enumerate(phis):
res += phi_j * data[t - j - 1]
data[t] = res
return data
|
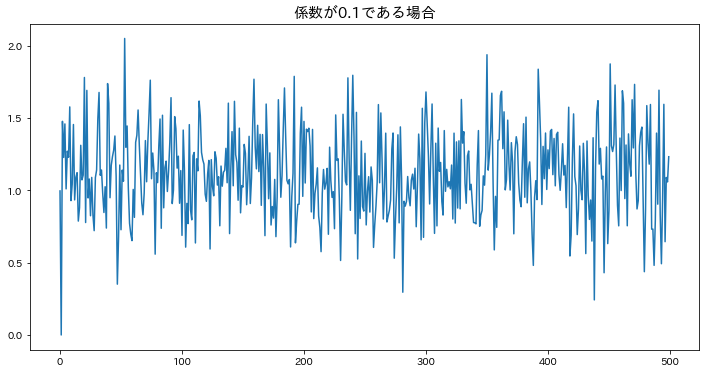
係数が1より小さい場合
#
1
2
3
4
5
6
| plt.figure(figsize=(12, 6))
phis = [0.1]
ar1_1 = create_ARdata(phis=phis)
plt.plot(ar1_1)
plt.title(f"係数が{phis[0]}である場合", fontsize=15)
plt.show()
|
==AR(1)過程の長さ500のデータを作成==
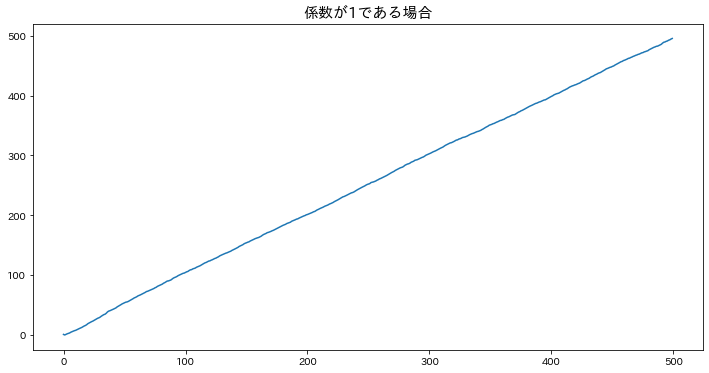
係数が1である場合
#
1
2
3
4
5
6
| plt.figure(figsize=(12, 6))
phis = [1]
ar1_2 = create_ARdata(phis=phis)
plt.plot(ar1_2)
plt.title(f"係数が{phis[0]}である場合", fontsize=15)
plt.show()
|
==AR(1)過程の長さ500のデータを作成==
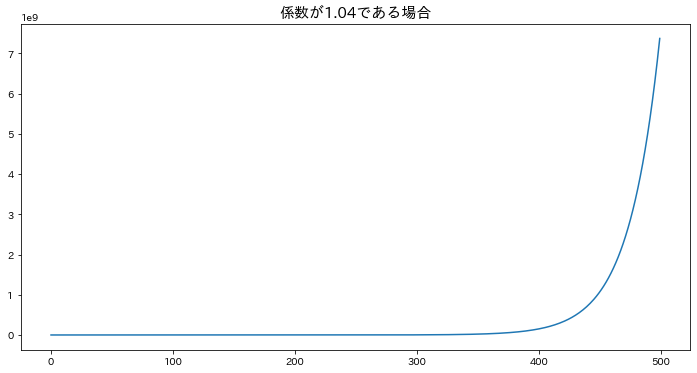
係数が1より大きい場合
#
1
2
3
4
5
6
| plt.figure(figsize=(12, 6))
phis = [1.04]
ar1_2 = create_ARdata(phis=phis)
plt.plot(ar1_2)
plt.title(f"係数が{phis[0]}である場合", fontsize=15)
plt.show()
|
==AR(1)過程の長さ500のデータを作成==
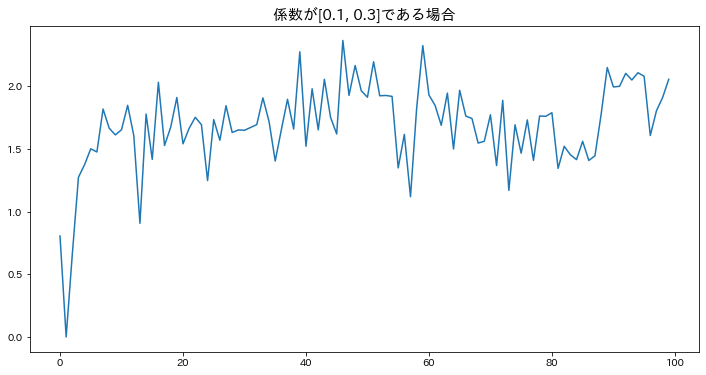
AR(2)
#
1
2
3
4
5
6
| plt.figure(figsize=(12, 6))
phis = [0.1, 0.3]
ar2_1 = create_ARdata(phis=phis, N=100)
plt.plot(ar2_1)
plt.title(f"係数が{phis}である場合", fontsize=15)
plt.show()
|
==AR(2)過程の長さ100のデータを作成==
1
2
3
4
5
6
| plt.figure(figsize=(12, 6))
phis = [0.1, -1.11]
ar2_1 = create_ARdata(phis=phis)
plt.plot(ar2_1)
plt.title(f"係数が{phis}である場合", fontsize=15)
plt.show()
|
==AR(2)過程の長さ500のデータを作成==

モデルの推定
#
1
2
3
4
5
6
| from statsmodels.tsa.ar_model import AutoReg
res = AutoReg(ar1_1, lags=1).fit()
out = "AIC: {0:0.3f}, HQIC: {1:0.3f}, BIC: {2:0.3f}"
print(out.format(res.aic, res.hqic, res.bic))
|
AIC: 231.486, HQIC: 236.445, BIC: 244.124
1
2
3
| print(res.params)
print(res.sigma2)
res.summary()
|
[1.03832755 0.07236388]
0.09199676371696269
AutoReg Model Results| Dep. Variable: | y | No. Observations: | 500 |
|---|
| Model: | AutoReg(1) | Log Likelihood | -112.743 |
|---|
| Method: | Conditional MLE | S.D. of innovations | 0.303 |
|---|
| Date: | Sat, 13 Aug 2022 | AIC | 231.486 |
|---|
| Time: | 01:55:17 | BIC | 244.124 |
|---|
| Sample: | 1 | HQIC | 236.445 |
|---|
| 500 | | |
|---|
| coef | std err | z | P>|z| | [0.025 | 0.975] |
|---|
| const | 1.0383 | 0.052 | 20.059 | 0.000 | 0.937 | 1.140 |
|---|
| y.L1 | 0.0724 | 0.045 | 1.621 | 0.105 | -0.015 | 0.160 |
|---|
Roots | Real | Imaginary | Modulus | Frequency |
|---|
| AR.1 | 13.8190 | +0.0000j | 13.8190 | 0.0000 |
|---|




