ラグプロットで自己相関の癖を掘る

中級

6.7.24

ラグプロットで自己相関の癖を掘る

最終更新 2020-03-14 読了時間 1 分
まとめ
  • ラグプロットで時系列の1期前の値と現在値を散布図にし、自己相関の強さを確認する。
  • ax.scatter でラグ散布図を描き、np.corrcoef で相関係数を算出する。
  • トレンドの持続性や特徴量選択の前段階として、時系列の依存構造を把握したいときに使う。

時系列の自己相関を見つけるには、1期前の値と現在値を散布図にしたラグプロットが有効です。右上がりであれば自己相関が強く、パターンが読めます。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

import numpy as np
import matplotlib.pyplot as plt

rng = np.random.default_rng(11)
series = np.cumsum(rng.normal(0, 1.2, size=120)) + 50
lag = 1

x_prev = series[:-lag]
x_curr = series[lag:]

fig, ax = plt.subplots(figsize=(4.4, 4.4))
ax.scatter(x_prev, x_curr, color="#38bdf8", alpha=0.7)

coef = np.corrcoef(x_prev, x_curr)[0, 1]
ax.set_xlabel("1期前の値")
ax.set_ylabel("現在の値")
ax.set_title(f"ラグ{lag}の散布図（相関係数 {coef:.2f}）")
ax.grid(alpha=0.2)

lims = [min(series) - 2, max(series) + 2]
ax.plot(lims, lims, color="#475569", linestyle="--", linewidth=1)
ax.set_xlim(lims)
ax.set_ylim(lims)

fig.tight_layout()

plt.show()

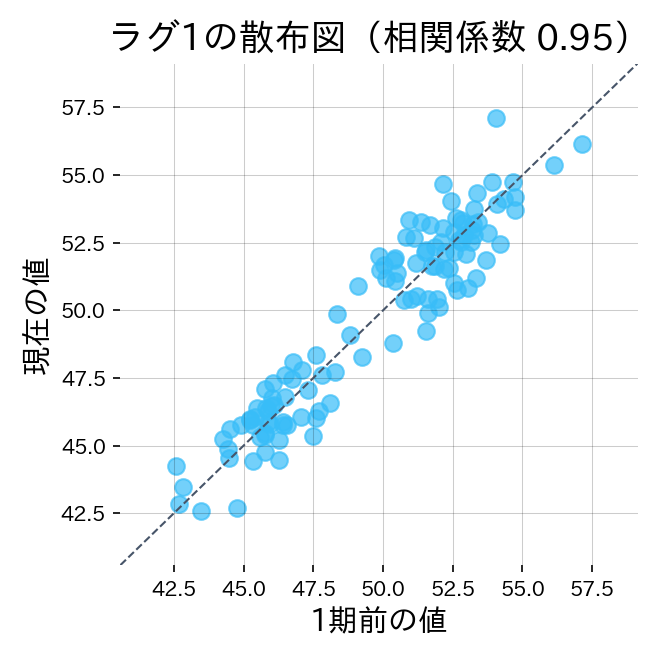
右上がりであれば自己相関が強く、パターンが読めますの図

読み方のポイント #

  • 点が右上がりに並ぶほど自己相関が強いサインです。トレンドが続く傾向にあると判断できます。
  • 円状に広がるなら自己相関が弱く、ランダムウォークに近い挙動だと推測できます。
  • 複数のラグを小さな multiples で並べると、どの遅れを特徴量に使うべきか判断しやすくなります。

いつ使うか #

  • 適している場面: 時系列データの自己相関の有無を視覚的にチェックしたいとき。ラグ1で強い正相関なら持続性を示唆します。
  • 不向きな場面: ラグの選び方が不適切だと有用な自己相関を見逃す恐れがあり、複数ラグを試す必要があります。
  • 代替手段: ACFプロット（自己相関関数プロット）を使えば全ラグの相関を一覧でき効率的です。

よくある失敗パターン #

  • ラグ次数の選択が恣意的: ラグ 1 だけを見て自己相関がないと判断するのは危険です。複数のラグ（1, 7, 30 等）を試して周期性を確認してください。
  • トレンドの影響を除去していない: 上昇トレンドがあるデータではラグプロットに疑似的な正相関が出ます。差分や対数変換でトレンドを除去してから確認しましょう。