Regresión lineal

Actualizado 2020-01-29 Lectura 3 min

Resumen

La regresión lineal modela la relación lineal entre entrada y salida y sirve como base tanto para la predicción como para la interpretación.
El método de mínimos cuadrados ordinarios estima los coeficientes minimizando la suma de los residuos al cuadrado y ofrece una solución en forma cerrada.
La pendiente indica cuánto cambia la salida cuando la entrada aumenta una unidad, mientras que la ordenada al origen representa el valor esperado cuando la entrada es cero.
Cuando el ruido o los valores atípicos son grandes conviene combinar estandarización y variantes robustas para mantener fiable el preprocesamiento y la evaluación.

Intuicion #

Este metodo se entiende mejor al conectar sus supuestos con la estructura de los datos y su efecto en la generalizacion.

Explicacion Detallada #

Formulación matemática #

Un modelo lineal univariado se expresa como

$$ y = w x + b. $$

Al minimizar la suma de cuadrados de los residuos $\epsilon_i = y_i - (w x_i + b)$

$$ L(w, b) = \sum_{i=1}^{n} \big(y_i - (w x_i + b)\big)^2, $$

obtenemos la solución analítica

$$ w = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n} (x_i - \bar{x})^2}, \qquad b = \bar{y} - w \bar{x}, $$

donde $\bar{x}$ y $\bar{y}$ son las medias de $x$ y $y$. La misma idea se extiende a la regresión multivariante usando vectores y matrices.

Experimentos con Python #

El siguiente ejemplo ajusta una recta con scikit-learn y dibuja el resultado. El código es el mismo que en la versión japonesa para mantener las figuras sincronizadas.

from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

def plot_simple_linear_regression(n_samples: int = 100) -> None:
    """Plot a fitted linear regression model for synthetic data.

    Args:
        n_samples: Number of synthetic samples to generate.
    """
    japanize_matplotlib.japanize()
    rng = np.random.default_rng(seed=0)

    X: np.ndarray = np.linspace(-5.0, 5.0, n_samples, dtype=float)[:, np.newaxis]
    noise: np.ndarray = rng.normal(scale=2.0, size=n_samples)
    y: np.ndarray = 2.0 * X.ravel() + 1.0 + noise

    model = make_pipeline(StandardScaler(with_mean=False), LinearRegression())
    model.fit(X, y)
    y_pred: np.ndarray = model.predict(X)

    fig, ax = plt.subplots(figsize=(10, 5))
    ax.scatter(X, y, marker="x", label="Observed data", c="orange")
    ax.plot(X, y_pred, label="Regression fit")
    ax.set_xlabel("$x$")
    ax.set_ylabel("$y$")
    ax.legend()
    fig.tight_layout()
    plt.show()

plot_simple_linear_regression()

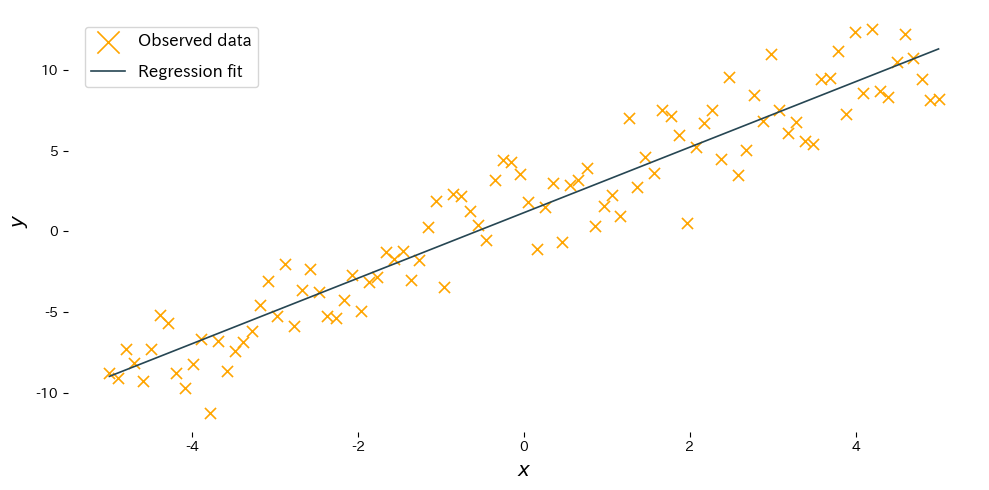
El código es el mismo que en la versión japonesa para manten… (figura)

Interpretación de los resultados #

Pendiente $w$: muestra cuánto aumenta o disminuye la salida cuando la entrada crece una unidad; la estimación debería acercarse al valor real.
Ordenada $b$: representa el valor esperado cuando la entrada es 0 y ajusta la posición vertical de la recta.
Estandarizar las características con StandardScaler estabiliza el aprendizaje cuando las escalas de entrada difieren.

Referencias #

Draper, N. R., & Smith, H. (1998). Applied Regression Analysis (3rd ed.). John Wiley & Sons.
Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning. Springer.